Coordinate Mondo e Coordinate Camera

Figura 8.2: Coordinate Immagine (Image coordinates)
Figura 8.3: Coordinate Camera (Camera coordinates)
Figura 8.4: Esempio di coordinate “Veicolo” o “Mondo”: Front-Left-Up o ISO 8855 (World coordinates)

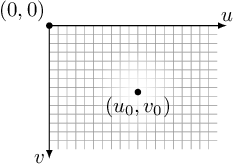
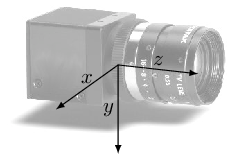
Quando si opera su problemi pratici risulta necessario passare da un sistema di riferimento solidale con la camera, dove il punto $(0,0,0)^{\top}$ coincide con il fuoco (pin-hole), a un sistema di riferimento più generico, che meglio si adatti alle esigenze dell'utilizzatore, dove la camera è posizionata in un punto generico del “mondo” e orientata rispetto ad esso in modo arbitrario. Questo discorso si applica a qualsiasi sensore generico, anche non video, definendo delle relazioni che permettono di passare i punti da coordinate mondo a coordinate sensore e viceversa.

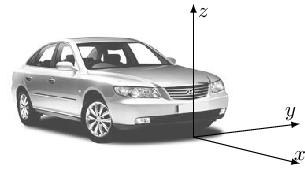
È necessario a questo punto fare una precisazione sulla terminologia legata ai sistemi di riferimento in questo libro: viene definito come sistema di riferimento “mondo” il sistema che di volta in volta è considerato assoluto e fisso, rispetto al quale viene posizionato il sensore. In figura 8.4 per esempio l'origine del sistema “mondo” è associato a un punto del veicolo (il punto frontale per esempio). In questo caso il sistema “veicolo” (body) o “mondo” (world) sono sinonimi. Questa distinzione però viene meno nel caso in cui ci sia un veicolo in movimento rispetto a un “mondo” che nuovamente si può definire il sistema di riferimento fisso. In tal caso avremo le coordinate sensore, quelle locali del veicolo/body e infine quelle del mondo. Solitamente però il sistema di assi che contraddistingue sensore, veicolo e mondo viene mantenuto consistente.

Se in coordinate camera il ruolo speciale che assume la coordinata $z$ è dovuto a motivazioni puramente matematiche, ovvero all'uso di coordinate omogenee che in fase di proiezione obbliga la divisione delle prime due componenti per la terza, in coordinate “sensore” questo limite viene meno. Anche se non vincolante in nessuna maniera, in questo libro è usato come sistema “sensore”, “body” e “mondo” quello presentato in figura 8.4 (ISO 8855) che assegna all'asse $z$ l'altezza del punto dal suolo.

Pertanto, per arrivare all'equazione definitiva della pin-hole camera si parte dall'equazione (8.4) e si applicano le seguenti considerazioni

• gli assi sono scambiati tra loro attraverso una permutazione $\boldsymbol\Pi$ (che è comunque una rotazione) per ottenere il sistema di riferimento finale;
• il sensore deve essere ruotato attraverso una trasformazione $\prescript{w}{}{\mathbf{R}}_{b}$ e di conseguenza non coincide con gli assi del sistema di riferimento “mondo”;
• il pin-hole non coincide ora con il punto $(0,0,0)^{\top}$ ma giace in un generico punto $\mathbf{t}_{0} = (x_{0}, y_{0}, z_{0})^{\top}$ espresso in coordinate mondo.

La conversione da coordinate “mondo” a coordinate “camera”, essendo una composizione di rotazioni, è anche essa una rotazione di equazione $\mathbf{R} = \prescript{c}{}{\mathbf{R}}_{w} = \boldsymbol\Pi \prescript{w}{}{\mathbf{R}}^{-1}_{b}$.

Sia $(x_{i},y_{i},z_{i})^{\top}$ un punto in coordinate “mondo” e $(\tilde{x}_{i},\tilde{y}_{i},\tilde{z}_{i})^{\top}$ il medesimo punto in coordinate “camera”. La relazione che lega questi due punti si può scrivere come

$$\begin{bmatrix} \tilde{x}_{i} \\ \tilde{y}_{i} \\ \tilde{z... ..._{i} \\ y_{i} \\ z_{i} \end{bmatrix} + \tilde{\mathbf{t}}_0$$ (8.15)

dove $\mathbf{R}$ è una matrice $3 \times 3$ che converte da coordinate mondo a coordinate camera, tiene conto delle rotazioni e della variazione del segno degli assi tra coordinate mondo e coordinate camera (vedi appendice A), mentre il vettore

$$\tilde{\mathbf{t}}_{0} = -\mathbf{R} \mathbf{t}_0$$ (8.16)

rappresenta la posizione del pin-hole $\mathbf{t}_0$ rispetto all'origine del sistema mondo, rappresentato però nel sistema di coordinate camera.

Va ricordato che le matrici di rotazione sono matrici ortonormali: hanno determinante 1, conservano pertanto distanze e aree, e l'inversa di una matrice di rotazione è la sua trasposta.

La matrice $\mathbf{R}$ e il vettore $\mathbf{t}_{0}$ possono venire accorpati in forma di matrice $3\times4$ sfruttando le coordinate omogenee. Grazie a questa rappresentazione, è possibile scrivere in maniera estremamente compatta la proiezione di un punto, espresso in coordinate mondo, omogenee a $(x_{i},y_{i},z_{i})^{\top}$, in un punto di coordinate immagine, omogenee a $(u_{i},v_{i})^{\top}$:

$$\lambda \begin{bmatrix} u_{i} \\ v_{i} \\ 1 \end{bmatri... ...] \begin{bmatrix} x_{i} \\ y_{i} \\ z_{i} \\ 1 \end{bmatrix}$$ (8.17)

Da questa equazione risulta abbastanza esplicito che ad ogni punto dell'immagine $(u_{i},v_{i})$ sono associati infiniti punti del mondo $(x_{i},y_{i},z_{i})^{\top}$ che vivono su una retta al variare del parametro $\lambda$.

Sottointendendo $\lambda$ e raccogliendo le matrici si ottiene l'equazione finale della pin-hole camera (che non tiene, né deve tener conto, della distorsione):

$$\begin{bmatrix} u_{i} \\ v_{i} \\ 1 \end{bmatrix} = \mathb... ...} \begin{bmatrix} x_{i} \\ y_{i} \\ z_{i} \\ 1 \end{bmatrix}$$ (8.18)

avendo definito $\mathbf{P} = \mathbf{K} [ \mathbf{R} \vert \mathbf{\tilde{t}}_0 ]$ matrice proiettiva (camera matrix) che verrà usata in seguito (Str87). La matrice $\mathbf{P}$ è una matrice $3\times4$ ed, essendo rettangolare, non è invertibile.

È da sottolineare che ponendo un vincolo aggiuntivo sui punti, per esempio $z_{i}=0$, la matrice $\mathbf{P}$ si riduce a una matrice $3 \times 3$, invertibile, che è esattamente la matrice omografica (vedi sezione 8.3.1) della trasformazione prospettica dei punti del suolo. La matrice $\mathbf{P}_{z=0}$ è un esempio di trasformazione IPM (Inverse Perspective Mapping) per ottenere una vista dall'alto (Bird eye view) della scena inquadrata (MBLB91).

La relazione inversa di quella di equazione (8.17), che trasforma punti immagine in coordinate mondo, si può scrivere come:

$$\begin{bmatrix} x_{i} \\ y_{i} \\ z_{i} \end{bmatrix}= \l... ...\mathbf{t}_0 = \lambda \mathbf{v}(u_{i}, v_{i}) + \mathbf{t}_0$$ (8.19)

dove risulta ben evidente che a ogni punto dell'immagine corrisponde una retta (al variare di $\lambda$) nel mondo che passa per il pin-hole ($\mathbf{t}_0$) e diretta nella direzione

$$\mathbf{v}(u_i,v_i) = \mathbf{R}^{-1} \mathbf{K}^{-1} \begin{bmatrix} u_{i} \\ v_{i} \\ 1 \end{bmatrix}$$ (8.20)

con $\mathbf{v}: \mathbb{R}^2 \to \mathbb{R}^3$ funzione che associa a ogni punto immagine il vettore che congiunge il pin-hole con il punto sensore corrispondente.

Usando direttamente la Camera Matrix $\mathbf{P} = \left[ \mathbf{P}_{3 \times 3} \vert \mathbf{p}_4 \right]$ è possibile ottenere un risultato equivalente all'equazione (8.19) nella forma

$$\begin{bmatrix} x_{i} \\ y_{i} \\ z_{i} \end{bmatrix}= \l... ... \\ 1 \end{bmatrix}- \mathbf{P}_{ 3\times 3}^{-1}\mathbf{p}_4$$ (8.21)

in modo da non usare esplicitamente le matrici dei parametri intrinseci ed estrinseci. Le due formulazioni sono ovviamente equivalenti.