Next: Trasformazioni omografiche notevoli Up: Coordinate Mondo e Coordinate Previous: Proprietà della matrice di
Possiamo usare la matrice di rotazione e l'equazione della pin-hole (8.18) per mostrare qualche risultato notevole.
Definiamo, dal sistema, la funzione ![]() di
di
![]() in
in
![]() chiamata perspective mapping definita come:
chiamata perspective mapping definita come:
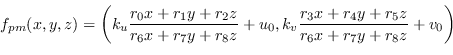 |
(8.24) |
Per ogni immagine esistono 3 punti di fuga, strettamente legati alla scelta degli assi di riferimento.
Prendiamo per esempio il primo asse. Nel nostro sistema di riferimento la coordinata ![]() è la distanza (per le altre 2 coordinate il discorso è similare).
Portiamo tale coordinata a infinito mantenendo le altre costanti. Quello che si ottiene è il punto
è la distanza (per le altre 2 coordinate il discorso è similare).
Portiamo tale coordinata a infinito mantenendo le altre costanti. Quello che si ottiene è il punto
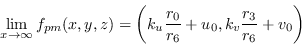 |
(8.25) |
Usando le matrici omogenee è possibile ottenere lo stesso risultato, con un formalismo più compatto.
Prendendo la trasformazione prospettica (8.17) e mandando via via
![]() ,
,
![]() e
e
![]() , i punti immagine (in coordinate omogenee) che si ottengono,
rappresentati i punti di fuga nelle 3 direzioni, sono esattamente le colonne della matrice
, i punti immagine (in coordinate omogenee) che si ottengono,
rappresentati i punti di fuga nelle 3 direzioni, sono esattamente le colonne della matrice
![]() , ovvero :
, ovvero :
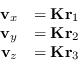 |
(8.26) |
In particolare, ponendosi nel caso semplificato ![]() ,
, ![]() e
e ![]() , i punti di fuga si trovano in
, i punti di fuga si trovano in
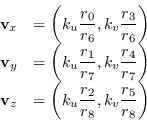 |
(8.27) |
È da notare che siccome le 3 colonne di ![]() sono ortonormali basta conoscere 2 punti di fuga per ottenere sempre il terzo (vedi sezione precedente).
sono ortonormali basta conoscere 2 punti di fuga per ottenere sempre il terzo (vedi sezione precedente).
Se mandiamo a infinito non una variabile ma più di una otteniamo più di un punto.
Per ![]() ma con
ma con ![]() il vanishing point degenera in una linea di equazione
il vanishing point degenera in una linea di equazione
| (8.28) |
Come un punto nell'immagine proiettata degenera in una linea, una linea di equazione ![]() diventa nell'immagine proiettata
diventa nell'immagine proiettata
| (8.29) |
Paolo medici