Matrici di Rotazione

Figura A.1: Rappresentazione dell'applicazione di una rotazione ad un vettore e a un sistema di assi: a sinistra una Inner/Active/Alibi Transformation, a destra una Outer/Passive/Alias Transformation.

Le rotazioni sono trasformazione isometriche dello spazio euclideo ovvero che trasformano vettori preservandone la lunghezza e lasciano un luogo di punti inalterato nello spazio pari ad un iperpiano (il centro di rotazione nel caso bidimensionale o un asse di rotazione nel caso tridimensionale).

L'insieme di tutte le Matrici di Rotazione $SO(n)$ in $\mathbb{R}^n$ è definito come Speciale Ortogonale

$$SO(n) = \left\{ \mathbf{R} \in \mathbb{R}^{n} : \mathbf{R}... ...\top} \mathbf{R} = \mathbf{I}, \det \mathbf{R} = + 1 \right\}$$ (A.1)

ovvero $\mathbf{R}^{-1} = \mathbf{R}^{\top}$.

Esistono due possibili convenzioni per definire una matrice di rotazione: alcuni autori preferiscono scrivere la matrice che trasforma da coordinate sensore a coordinate mondo, altri invece l'opposto. La matrice stessa di rotazione ha la duplice veste di indicare una rotazione all'interno di un sistema di riferimento (Active o Alibi), o la trasformazione di coordinate da un sistema di riferimento a un secondo sistema di riferimento (Passive o Alias).

In questo libro le matrici sono prevalentemente usate per rappresentare cambi di base e, quando possibile, il sistema di riferimento sorgente e quello di destinazione sono ben evidenziati.

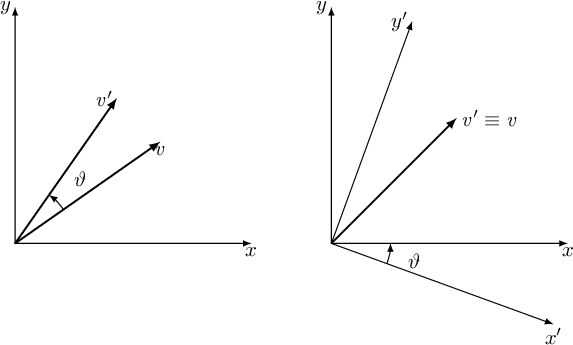
Per discutere delle matrici di rotazione e fare qualche considerazione interessante risulta comodo partire ad analizzare il caso bidimensionale, schematizzato in figura A.1.

Si può verificare che $SO(2)$ ha un solo grado di libertà. La matrice $\mathbf{R}_{\vartheta}$, che rappresenta una rotazione bidimensionale, può essere scritta nella forma

$$\mathbf{R}_{\theta} = \begin{bmatrix} \cos \vartheta & -... ...eta \\ \sin \vartheta & \cos \vartheta \\ \end{bmatrix}$$ (A.2)

Come si può vedere dalla figura A.1 quando si parla di una rotazione di un angolo $\vartheta$ la stessa trasformazione può essere vista in modi differenti, a seconda di quale sistema di riferimento l'osservatore si posizioni solidale. La matrice $\mathbf{R}_{\theta}$ permette di ruotare un vettore in senso antiorario (rispetto all'origine del sistema di riferimento) di un angolo $\vartheta$ (figura a sinistra in A.1) ^A.1. La matrice di forma (A.2) oltre che a ruotare un vettore in senso antiorario permette anche di ottenere le cosidette coordinate “mondo” di un punto conoscendo la coordinate “sensore” e sapendo che tale sensore è ruotato di un angolo $\vartheta$ (legge della mano destra) nel sistema di riferimento “mondo”. La matrice (A.2) permette perciò di passare da coordinate “sensore” a coordinate “mondo”, mentre l'inversa di questa matrice permette di passare da coordinate “mondo” a coordinate “sensore”.

La distinzione tra Inner/Active/Alibi Transformation e Outer/Passive/Alias Transformation è un altro modo per descrivere la differenza tra rotazioni. Questi termini sono spesso utilizzati in contesti matematici e fisici per chiarire se una trasformazione agisce sul sistema di riferimento stesso (il sistema di riferimento viene ruotato o traslato, mentre gli oggetti rimangono fissi nello spazio, perciò alias o passive) o sugli oggetti all'interno di un sistema di riferimento fisso (gli oggetti vengono ruotati o traslati, mentre il sistema di riferimento rimane invariato, perciò alibi o active).

La matrice di rotazione viene anche chiamata Matrice dei Coseni Direzionali (Direction Cosine Matrix, DCM) in quanto le colonne della matrice di trasformazione corrispondono alle matrici dei coefficienti dei vecchi vettori base espressi rispetto alla nuova base.

In questo libro, lavorando di fatto con sensori (e non con bracci robotici), tutte le matrici sono di fatto matrici di cambiamento di base in quanto si vuole principalmente conoscere la coordinata di un punto di visto da un sensore nel sistema di riferimento superiore o viceversa.

Passando al caso tridimensionale il discorso si complica ulteriormente: esistono infinite parametrizzazioni per esprimere una rotazione partendo da 3 parametri $\mathbf{so}(3)$.

È per esempio possibile definire una rotazione come composizione di 3 rotazioni elementari intorno a uno dei 3 assi ma essendo la moltiplicazione tra matrici non commutativa esistono comunque 24 modi per comporre tra loro queste 3 matrici. Le combinazioni di matrici vengono indicate come sequenze di Eulero seguite da 3 numeri per indicare l'ordine di combinazione delle rotazioni: 1 per l'asse $x$, 2 per l'asse $y$ e 3 per l'asse $z$. In ambito robotico sono ampiamente diffuse la rappresentazione di Angoli di Eulero (sequenza ZYZ) o quella degli angoli di Tait-Bryan (sequenza di Eulero 321 o ZYX) e si veda la sezione seguente A.1 per i dettagli^A.2. Nella letteratura italiana i sei gruppi (XYZ, YZX, ZXY, XZY, ZYX, YXZ) vengono definiti angoli di Cardano.

Questo sistema di angoli tuttavia presenta alcune singolarità che ne limitano l'utilizzo. Alternativamente la sintassi proposta da Rodrigues (sezione A.2) o i quaternioni (sezione A.3) possono essere usati per superare questo problema.

Sempre per il fatto che il prodotto delle matrici non è commutativo, nello spazio tridimensionale c'è addirittura un ulteriore livello di ambiguità dato dall'ordine con cui le rotazioni con angoli di eulero vengono descritte, in quanto le rotazioni possono essere definite estrinseche o intrinseche:

Rotazioni Estrinseche

Si riferiscono a rotazioni attorno ad assi fissi che coincidono con il sistema di riferimento iniziale dell'oggetto in rotazione. Gli assi di riferimento rimangono invariati durante le rotazioni. Le sequenze di rotazione estrinseche sono specificate da notazioni come x-y-z.

Rotazioni Intrinseche

Si riferiscono a rotazioni attorno ad assi mobili che sono attaccati all'oggetto in rotazione. Questi assi cambiano posizione dopo ogni rotazione. Le sequenze di rotazione intrinseche sono specificate da notazioni come x-y'-z”, dove gli apici indicano i nuovi sistemi di riferimento successivi.

Una rotazione estrinseca equivale ad una rotazione intrinseca (e viceversa) ma con l'ordine di composizione delle trasformazioni invertito (e.g. una trasformazione estrinseca z-y-x equivale ad una intrinseca x-y'-z”).

Indipendentemente dal significato geometrico a cui si vuole dare la matrice di rotazione è possibile comunque fare diverse considerazioni.

Come già detto in precedenza, la definizione della matrice $\mathbf{R}$ nell'equazione della pin-hole camera è stata definita, sia per comodità che per tradizione, in modo tale da non ruotare un vettore (sarebbe stata ovvero una conversione da coordinate “sensore” a coordinate “mondo”) ma all'opposto rimuove la rotazione di punti del mondo conoscendo l'orientazione della camera stessa ovvero permette di convertire da coordinate “mondo” a coordinate “camera”.

Ricavare una espressione della matrice $\mathbf{R}$ nella forma espressa nel modello della pin-hole camera vuol dire trovare una matrice che trasforma un punto da coordinate “mondo” a coordinate “camera” ovvero bisogna sempre usare la matrice inversa delle matrici di rotazioni che si possono trovare nelle sezioni seguenti.

Sia pertanto una generica rotazione $\prescript{w}{}{\mathbf{R}}_{b}$ che trasforma da coordinate locali, mobili, “sensore” (body coordinates nel caso generico) a coordinate globali, fisse, “mondo”: la matrice $\left( \prescript{w}{}{\mathbf{R}}_{b} \right)^{-1} = \prescript{b}{}{\mathbf{R}}^{}_{w}$ sarà pertanto la matrice che converte da coordinate mondo a coordinate sensore.

Siccome però il sistema di riferimento camera/immagine è un sistema Left-Bottom-Front (X crescente verso destra, Y crescente verso il basso, Z la profondità come in figura 8.3) che è diverso dal sistema di riferimento Front-Left-Up sensore/mondo (Z crescente verso l'alto, X profondità e Y crescente verso sinistra come in figura 8.4) tipico dell'ambiente automotive, è necessario definire una matrice

$$\prescript{c}{}{\boldsymbol\Pi_{b}} = \begin{bmatrix} 0 & -1 & 0 \\ 0 & 0 & -1 \\ 1 & 0 & 0 \end{bmatrix}$$ (A.3)

matrice di permutazione degli assi. La matrice di permutazione ha determinante +1 pertanto è ancora una rotazione che preserva la chiralità dello spazio (trasforma sistemi destrorsi in sistemi destrorsi).

Lavorando in ambito areonautico o navale potrebbe invece essere necessario passare dal sistema camera/immagine a un sistema Front-Right-Down (ad esempio il NED). In questa situazione la matrice di permutazione è

$$\prescript{c}{}{\boldsymbol\Pi_{b'}} = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{bmatrix}$$ (A.4)

Sotto queste considerazioni, la matrice $\mathbf{R}$ che converte da “mondo” a “camera”, formalismo usato normalmente nell'equazione della camera pin-hole, ha come espressione

$$\mathbf{R} = \prescript{c}{}{\mathbf{R}}_{w} = \prescript{... ...l\Pi_{b}} \left( \prescript{w}{}{\mathbf{R}}_{b} \right)^{-1}$$ (A.5)

Footnotes

...fig:rotation) ^A.1

Come già accennato all'inizio, bisogna fare attenzione perché la trasformazione inversa/trasposta, ovvero la matrice generata dall'angolo $-\vartheta$, in letteratura può essere indicata come “matrice di rotazione” e indicata anch'essa con la lettera $\mathbf{R}$.

... dettagli^A.2

Gli angoli Roll-Pitch-Yaw XYZ o semplicemente Roll-Pitch-Yaw sono spesso utilizzati in robotica e aeronautica; tuttavia per creare confusione questa è una rappresentazione intrinseca e sono equivalenti a quelli che a volte vengono chiamati angoli di Eulero ZYX dove invece viene usata una rappresentazione estrinseca.