Next: Modello Fish-Eye Camera Up: Matrici di Rotazione Previous: Rotazioni infinitesimali
Son: Well, Papa, can you multiply triplets?
Father: No [sadly shaking his head], I can only add and subtract them.
(William Rowan Hamilton, Conversation with his sons (1843))
I quaternioni sono un tentativo di estensione dei numeri complessi a una dimensione maggiore. Tale formulazione è stata proposta per la prima volta da Sir William Rowan Hamilton.
Sono rappresentati da un vettore di
![]() nella forma
nella forma
 .
I quaternioni hanno differenti proprietà rispetto agli ordinari vettori quadridimensionali (come per esempio lo sono anche le coordinate omogenee).
Il quaternione (A.18) può essere visto come composto da una parte vettoriale
.
I quaternioni hanno differenti proprietà rispetto agli ordinari vettori quadridimensionali (come per esempio lo sono anche le coordinate omogenee).
Il quaternione (A.18) può essere visto come composto da una parte vettoriale
 :
:
 |
(A.19) |
 è definita parte scalare (o componente reale) mentre
è definita parte scalare (o componente reale) mentre  sono le componenti vettoriali (o immaginarie).
Un quaternione con solo la parte scalare è chiamato reale mentre un quaternione con solo la parte vettoriale puro.
sono le componenti vettoriali (o immaginarie).
Un quaternione con solo la parte scalare è chiamato reale mentre un quaternione con solo la parte vettoriale puro.
Il prodotto tra quaternioni per esempio non è commutativo (ma è comunque associativo).
È possibile creare un vettore aumentato (augmented vector) di un vettore
![]() nello spazio dei quaternioni come:
nello spazio dei quaternioni come:
 |
(A.20) |
Il complesso coniugato di un quaternione
![]() è
è
 |
(A.21) |
La norma
![]() è
è
 |
(A.22) |
La proprietà più importante di un quaternione è che esso rappresenta una rotazione in ![]() .
.
Una rotazione
![]() , espressa in rappresentazione asse/angolo, può essere scritta sotto forma di quaternione
, espressa in rappresentazione asse/angolo, può essere scritta sotto forma di quaternione
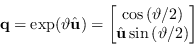 |
(A.23) |
 |
(A.24) |
Le rotazioni sono rappresentate da quaternioni di lunghezza unitaria
![]() .
.
È possibile ruotare un punto usando direttamente i quaternioni

 |
(A.25) |
 |
(A.26) |
 .
.
È da notare che ![]() e
e ![]() rappresentano la medesima matrice di rotazione
rappresentano la medesima matrice di rotazione ![]() .
.
Viceversa dalla matrice di rotazione è possibile ricavare il quaternione attraverso per esempio
 |
(A.27) |
Il prodotto tra due quaternioni rappresenta infine la composizione di rotazioni:
 |
(A.28) |
Paolo medici