Modello Fish-Eye Camera

Le ottiche fish-eye sono lenti dove la distorsione barilotto è dominante e questo permette di ottenere, a parità di lunghezza focale, angoli di vista molto elevati, fino a 180 gradi o superiori.

Nel modello della camera pin-hole il rapporto tra l'angolo incidente di luce e la coordinate del pixel segue la regola $r = f \tan \vartheta$.

Le lenti fish-eye seguono invece equazioni molto differenti, tra le quali è possibile segnalare tra i modelli teorici

• lineare: $r = f \vartheta$
• ortografica: $r = f \sin \vartheta$
• angolo solido costante: $r = 2 f \sin (\vartheta/2)$
• stereografica: $r = 2 f \tan ( \vartheta/2)$.

In assenza di distorsione, le equazioni sopra permettono di trasformare l'angolo di luce incidente sull'ottica in un raggio proiettato sul sensore:

$$\begin{array}{l} x' = r \cos \varphi \\ y' = r \sin \varphi \\ \end{array}$$ (B.1)

dove $\varphi$, l'angolo di fase espresso in coordinate polari come in sezione 1.3.1, rimane costante tra raggio incidente e raggio proiettato.

Questa classe di modelli non tiene conto di eventuali non linearità dell'ottica. Il modello di Kannala-Brandt (KHB09) generalizza le equazioni viste sopra, parametrizzando una generica lente fish-eye come

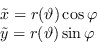$$\begin{array}{l} \tilde{x} = r(\vartheta) \cos \varphi \\ \tilde{y} = r(\vartheta) \sin \varphi \\ \end{array}$$ (B.2)

dove il termine $r(\vartheta)$ è la classica espansione in serie di Taylor che permette di inglobare sia i diversi modelli di lente presentati che eventuali distorsioni introdotte dell'ottica.