Next: Rotazioni infinitesimali Up: Matrici di Rotazione Previous: Angoli di Eulero
Ogni rotazione è equivalente a una rotazione intorno a un asse (di rotazione) di una certa quantità angolare. Da questo presupposto parte la formulazione di una rotazione di Rodrigues o Parametrizzazione Asse-Angolo. La formulazione di Rodrigues cerca di risolvere i problemi di singolarità intrinseci delle formulazioni di Tait-Bryan e Eulero (diverse combinazioni di valori rappresentano la stessa matrice di rotazione), oltre a fornire una formulazione geometrica e concisa della rotazione.
La formula della rotazione proposta da Rodrigues è formata da un versore ![]() e da un angolo
e da un angolo ![]() i quali permettono di rappresentare una rotazione dei punti dello spazio di un angolo
i quali permettono di rappresentare una rotazione dei punti dello spazio di un angolo ![]() , intorno all'asse formato dal vettore
, intorno all'asse formato dal vettore ![]() , con verso positivo nel senso della regola della mano destra.
, con verso positivo nel senso della regola della mano destra.
È possibile convertire asse e angolo in una matrice di rotazione attraverso una equazione compatta proposta da Rodrigues:
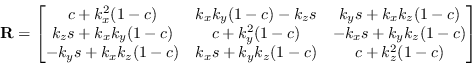 |
(A.14) |
La formulazione inversa è anch'essa estremamente compatta e vale:
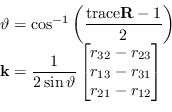 |
(A.15) |
Siccome ![]() e
e ![]() sono di fatto 4 parametri, solitamente si usa un vettore
sono di fatto 4 parametri, solitamente si usa un vettore
![]() generico per rappresentare una rotazione nella formulazione di Rodrigues e si attuano le sostituzioni:
generico per rappresentare una rotazione nella formulazione di Rodrigues e si attuano le sostituzioni:
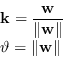 |
(A.16) |