Next: Coordinate Mondo e Coordinate Up: Pin-Hole Camera Previous: Pin-Hole Camera
La totalità delle telecamere commerciali devia dal modello della pin-hole camera e tale deviazione è generalmente tanto maggiore quanto grande è il campo visivo della camera: siccome ogni ottica è composta da un certo numero di lenti, la distorsione deriva dalle non idealità nella fase di produzione e di assemblaggio dell'ottica. Ottenere infatti una lente non distorcente è un processo estremamente costoso e soprattutto nelle applicazioni a basso costo dove bisogna fare affidamento a ottiche economiche risulta un problema molto evidente.
Queste non idealità generano una distorsione non lineare difficilmente modellizzabile e, anche per il fatto che tale distorsione dipende dall'interazione tra la lente e il sensore, i produttori di lenti normalmente non forniscono, o non riescono a fornire, informazioni geometriche su come rappresentare tale distorsione.
È importante osservare che il modello della pin-hole camera è valido solamente se l'immagine su cui si lavora è non distorta pertanto calibrare, ovvero correggere la distorsione geometrica, è un prerequisito per ricostruire in maniera accurata la tridimensionalità della scena osservata.
Dal punto di vista del raggio ottico, la distorsione introdotta dalla lente si pone tra il mondo e il pin-hole.
L'equazione della camera pin-hole modificata con la distorsione dell'ottica si trasforma in
| (8.7) |
Con questo formalismo la distorsione ![]() trasforma un punto da coordinate non-distorte in coordinate distorte.
Questa scelta, rispetto alla formulazione inversa, viene da considerazioni puramente pratiche:
siccome l'obiettivo è quello di avere un immagine in uscita densa e non-distorta (si veda la discussione in sezione 1.12), è necessario calcolare quella funzione che trasforma appunto un punto non-distorto in un punto distorto.
trasforma un punto da coordinate non-distorte in coordinate distorte.
Questa scelta, rispetto alla formulazione inversa, viene da considerazioni puramente pratiche:
siccome l'obiettivo è quello di avere un immagine in uscita densa e non-distorta (si veda la discussione in sezione 1.12), è necessario calcolare quella funzione che trasforma appunto un punto non-distorto in un punto distorto.
In generale i contributi distorcenti della lente si dividono in radiali (diretti lungo la direttrice che unisce il punto al centro di distorsione) o tangenziali (che sono perpendicolari alla direttrice). I contributi tangenziali (e altri contributi qui non citati) sono normalmente piccoli mentre la distorsione radiale è sempre rilevabile e, man mano che la focale diventa corta, in generale aumenta di intensità.
Questa sezione si occupa di ricavare una relazione generale tra il punto ideale ![]() e l'effettivo punto immagine distorto osservato
e l'effettivo punto immagine distorto osservato
![]() .
.
In tutta l'immagine esiste un solo punto ![]() , definito centro di distorsione, dove la distorsione non produce effetti.
Per questo punto
, definito centro di distorsione, dove la distorsione non produce effetti.
Per questo punto
![]() .
.
Per definire la distorsione è necessario operare in una nuova serie di coordinate, relative al centro di distorsione:
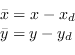 |
(8.8) |
La formulazione classica di Brown-Conrady (Bro66) modella la distorsione della lente sotto forma di scostamento:
Tali scostamenti possono essere suddivisi per contributi:
La funzione ![]() della distorsione radiale non è un modello conosciuto ma può essere approssimata attraverso i primi termini dello sviluppo in serie:
della distorsione radiale non è un modello conosciuto ma può essere approssimata attraverso i primi termini dello sviluppo in serie:
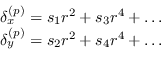 |
(8.12) |
Tali contributi sono spesso inadeguati tuttavia per descrivere gli effetti di decentramento dell'ottica.
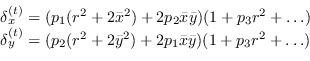 |
(8.13) |
Inserendo tutti questi contributi all'interno dell'equazione (8.9), il modello Brown-Conrady complessivo si scrive come
Per esempio OpenCV modella la distorsione con il modello R3P1: 3 termini radiali (![]() ,
, ![]() ,
, ![]() ) e il termine di decentramento di primo grado (
) e il termine di decentramento di primo grado (![]() ,
, ![]() ).
).
I coefficienti della distorsione sono ricavati con diverse tecniche disponibili in letteratura applicate ad immagini acquisite in ambiente strutturato (griglie di calibrazione). Normalmente viene usato un minimizzatore non lineare e, o si lavora su rette e si itera fino a che tutte le curve dell'immagine non diventino rette plumb-line method (DF01), o si forza che i punti su un piano di coordinate note rappresentino una omografia. Tali tecniche sono applicabili solamente se si opera in coordinate immagine (approccio 1).
Per calibrare la distorsione in coordinate camera normalizzate (approccio 2) bisogna che contemporaneamente distorsione e parametri intrinseci della camera vengano calcolati (Zha99). Una stima iniziale dei parametri intrinseci può venire da un minimizzatore lineare ma la stima finale si ottiene solo attraverso un minimizzatore non lineare.
La tecnica ampiamente usata per stimare i parametri della distorsione è ottimizzare l'osservazione di punti caratteristici sull'immagine la cui posizione in coordinate mondo è conosciuta in modo da forzare una proiezione prospettica completa (sezione 8.5.6).
Paolo medici