Next: Determinazione delle matrici Up: Visione Multicamera Previous: Camere inclinate rispetto a
Nel 1981, Christopher Longuet-Higgins (Lon81) osserva per primo che un generico punto espresso in coordinate mondo, i rispettivi punti in coordinate camera e i pin-hole devono essere tra loro coplanari. La derivazione geometrica delle relazioni che intercorrono tra i punti viene tralasciata ma viene presentata direttamente quella analitica.
È stato più volte ripetuto che un punto su un'immagine sottende una retta nel mondo, e la retta nel mondo proiettata su un altra immagine, acquisita da una camera posta in un punto di vista differente, rappresenta la retta epipolare dove giace l'omologo del punto della prima immagine. Tale equazione, che lega punti di un'immagine con rette nell'altra, può essere espressa attraverso una forma matriciale.
Per seguire il ragionamento di Higgins, la matrice dei parametri intrinseci verrà sottintesa e le coordinate usate saranno quelle camera normalizzate.
Senza perdere generalità, si consideri pertanto un sistema costituito da due camere, la prima posizionata e orientata rispetto alla seconda con matrice di proiezione
![$\mathbf{P}_1=[\mathbf{R}\vert\mathbf{t}]$](img34.svg)
![$\mathbf{P}_2=[\mathbf{I}\vert\mathbf{0}]$](img35.svg)

![]() , ovvero posizione della camera 1 rispetto al sistema 2.
, ovvero posizione della camera 1 rispetto al sistema 2.
Un generico punto
![]() ha coordinata
ha coordinata ![]() e
e ![]() nei due diversi sistemi di riferimento e viene proiettato sui sensori 1 e 2 nei punto in coordinate camera
nei due diversi sistemi di riferimento e viene proiettato sui sensori 1 e 2 nei punto in coordinate camera ![]() e
e ![]() rispettivamente.
rispettivamente.
Questi punti immagine sappiamo che sottendendo un sottospazio di ![]() di equazione per esempio
di equazione per esempio

![]() ) ovvero
) ovvero
 |
(9.36) |
Un generico punto

L'equazione della retta epipolare, retta in coordinate camera nel secondo sensore e luogo dei punti dove deve giacere ![]() , associata al punto
, associata al punto ![]() (osservato e pertanto espresso in coordinate camera del primo sensore), risulta essere
(osservato e pertanto espresso in coordinate camera del primo sensore), risulta essere
 (questo è un esempio di ricostruzione tridimensionale tramite triangolazione come si è visto in sezione 9.3.1).
(questo è un esempio di ricostruzione tridimensionale tramite triangolazione come si è visto in sezione 9.3.1).
Esiste tuttavia una relazione che mette in relazione i punti delle due camere cancellando i parametri ![]() ma soprattutto permette di fare il ragionamento inverso ovvero quello di ricavare la posa relativa tra le due camere
ma soprattutto permette di fare il ragionamento inverso ovvero quello di ricavare la posa relativa tra le due camere
![]() dato un elenco di punti omologhi.
dato un elenco di punti omologhi.
Se si moltiplicano entrambi i lati dell'equazione (9.38), prima vettorialmente per ![]() , poi scalarmente per
, poi scalarmente per
![]() , si ottiene infatti
, si ottiene infatti
 |
(9.39) |
Questo passaggio ha un significato fisico: vengono per prima di tutto inseriri i vincoli di coplanarità (tutti espressi per esempio nel reference 2) tra i punti ![]() (pinhole della camera 2),
(pinhole della camera 2), ![]() ,
,


![]() (pinhole della camera 1 nel sistema 2), e uniti con il fatto che il corpo è rigido.
(pinhole della camera 1 nel sistema 2), e uniti con il fatto che il corpo è rigido.
Attraverso questa formula, è possibile esprimere le relazioni che intercorrono tra i punti omologhi ![]() e
e ![]() , rappresentati sotto forma di coordinate camera omogenee, in una forma molto compatta
, rappresentati sotto forma di coordinate camera omogenee, in una forma molto compatta
Bisogna infine stare molto attenti agli indici perché non c'è una convenzione unica per indicare i punti 1 e 2: supponendo la convenzione (9.41) soddisfatta quello che bisogna ricordarsi è che matrice ![]() codifica la posa relativa della camera dei punti a destra (nel nostro caso
codifica la posa relativa della camera dei punti a destra (nel nostro caso ![]() ) della matrice
) della matrice ![]() rispetto alla camera dei punti a sinistra (nel nostro caso
rispetto alla camera dei punti a sinistra (nel nostro caso ![]() ) della matrice.
) della matrice.
La matrice ![]() , mettendo in relazioni punti omogenei, è anch'essa omogenea e pertanto definita a meno di un fattore moltiplicativo.
, mettendo in relazioni punti omogenei, è anch'essa omogenea e pertanto definita a meno di un fattore moltiplicativo.
La matrice Essenziale ha le seguenti proprietà:
La matrice Essenziale crea delle relazioni in coordinate camera e pertanto, per poterla utilizzare da un punto di vista pratico, è necessario avere a disposizione punti espressi in questo particolare sistema di riferimento, ovvero è necessario conoscere i parametri intrinseci delle camere coinvolte.
L'equazione
| (9.43) |
È tuttavia possibile introdurre una ulteriore relazione tra i punti delle immagini, trascurando completamente i parametri intrinseci delle camere stesse.
Se si applica la definizione di coordinate camera omogenee
![]() nella relazione (9.42) si ottiene
nella relazione (9.42) si ottiene
La matrice Fondamentale (Fundamental matrix) è definita (Faugeras e Hartley, 1992) come:
Se due punti sulle due immagini della coppia stereoscopica rappresentano lo stesso punto nel mondo, l'equazione (9.45) deve essere soddisfatta.
La matrice fondamentale permette di restringere l'intervallo di ricerca di corrispondenze tra le due immagini in quanto, per il dualismo punto-retta, dalla relazione (9.45) si può esplicitare il luogo dei punti nella seconda immagine dove cercare i punti della prima.
Infatti l'equazione di una linea dove i punti ![]() ed
ed ![]() devono vivere è descritta da
devono vivere è descritta da
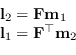 |
(9.46) |
La relazione che intercorre tra la matrice Fondamentale e la matrice Essenziale risulta essere, equazione (9.44),
| (9.47) |
| (9.48) |
La matrice Essenziale raccoglie in sxE9 le pose relativa tra le camere, mentre la matrice Fondamentale nasconde sia i parametri intrinseci che la posa relativa.
La matrice Essenziale introduce vincoli uguali a quelli della matrice Fondamentale ma, anche se introdotta storicamente prima della matrice Fondamentale, ne è un caso particolare perchxE9 esprime le relazioni rispetto a coordinate camera.
![]() è una matrice
è una matrice ![]() di rango 2 e per essere determinata bastano 7 punti, in quanto i gradi di libertà risultano essere appunto solamente 7 (un fattore moltiplicativo e il determinante nullo riducono la dimensione del problema).
La relazione che lega la matrice Fondamentale ai 7 gradi di libertà è una relazione non lineare (relazione non facilmente esprimibile attraverso una qualche rappresentazione algebrica).
Con (almeno) 8 punti si riesce invece ad ottenere una stima lineare della matrice, come descritto nella sezione successiva.
di rango 2 e per essere determinata bastano 7 punti, in quanto i gradi di libertà risultano essere appunto solamente 7 (un fattore moltiplicativo e il determinante nullo riducono la dimensione del problema).
La relazione che lega la matrice Fondamentale ai 7 gradi di libertà è una relazione non lineare (relazione non facilmente esprimibile attraverso una qualche rappresentazione algebrica).
Con (almeno) 8 punti si riesce invece ad ottenere una stima lineare della matrice, come descritto nella sezione successiva.
La matrice Fondamentale ha le seguenti proprietà:

|
Le matrici Fondamentale ed Essenziale possono essere usate per restringere il campo di ricerca dei punti omologhi tra due immagini e/o filtrare via eventuali outlier (ad esempio in RANSAC). La matrice Essenziale, se decomposta, permette di ricavare la posa relativa tra le due camere e in quanto tale dare una idea, approssimata, del movimento che ha subito una camera che si sposta nel mondo (motion stereo) o della posa relativa di due camere in una coppia stereoscopica (Auto-Calibrazione).
L'uso della matrice Essenziale permette di ricavare la posa relativa tra due viste. Non è però possibile conoscere la lunghezza della baseline che unisce i due pin-hole, ma solo la sua direzione. Tuttavia, avendo a disposizione la matrice Essenziale, è sempre possibile eseguire una ricostruzione tridimensionale della scena osservata a meno di un fattore moltiplicativo: i rapporti tra le distanze sono conosciuti, ma non il loro valore assoluto. Questo permette però, quando si osserva la medesima scena da più di due viste differenti, una ricostruzione tridimensionale coerente, dove per tutte le viste il fattore moltiplicativo sconosciuto rimane sempre lo stesso, permettendo perciò di fondere tutte le singole ricostruzioni in un'unica ricostruzione conosciuta a meno del medesimo fattore di scala.