Next: Ricostruzione con camere rettificate Up: Ricostruzione tridimensionale Previous: Ricostruzione tridimensionale
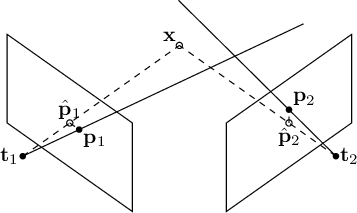 |
Osservando la figura 9.2 è facile intuire che la soluzione del problema della triangolazione è il punto di incontro delle rette epipolari generate dalle due immagini.
Tale problema può essere facilmente esteso al caso di ![]() camere dove la posa relativa tra di loro è conosciuta. In mancanza della conoscenza della posa assoluta questa potrebbe essere ottenuta direttamente dalle immagini stesse usando tecniche come la matrice Essenziale (sezione 9.4).
camere dove la posa relativa tra di loro è conosciuta. In mancanza della conoscenza della posa assoluta questa potrebbe essere ottenuta direttamente dalle immagini stesse usando tecniche come la matrice Essenziale (sezione 9.4).
A causa delle imprecisioni di individuazione dei punti omologhi (un discorso a parte si potrebbe fare per gli errori di calibrazione) le rette formate dai raggi ottici sono in genere sghembe.
In tal caso è necessario ricavare la soluzione più vicina sotto qualche funzione di costo: la soluzione ai minimi quadrati è possibile sempre con ![]() , sia con tecniche come la Forward Intersections o la Direct Linear Transfer DLT.
, sia con tecniche come la Forward Intersections o la Direct Linear Transfer DLT.
Ogni raggio ottico sotteso al pixel immagine ![]() , con
, con
![]() la vista i-esima, deve soddisfare l'equazione (9.7).
Il punto di intersezione (Forward Intersections) di tutti questi raggi è la soluzione di un sistema lineare, potenzialmente sovradimensionato, con
la vista i-esima, deve soddisfare l'equazione (9.7).
Il punto di intersezione (Forward Intersections) di tutti questi raggi è la soluzione di un sistema lineare, potenzialmente sovradimensionato, con ![]() incognite in
incognite in ![]() equazioni:
equazioni:
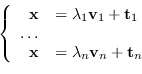 |
(9.11) |
La soluzione in forma chiusa, limitata al caso di sole due rette, è disponibile in sezione 1.5.8. Questa tecnica si può applicare al caso di una camera allineata con gli assi e la seconda posizionata relativamente alla prima in accordo con la relazione (9.3).
Sfruttando le proprietà del prodotto vettoriale, si può arrivare alla stessa espressione usando le matrici di proiezione prospettica e i punti immagine, espressi sotto forma di coordinate omogenee:
![\begin{displaymath}
\left\{
\begin{array}{l}
\left[ \mathbf{p}_{1} \right]_{\tim...
...right]_{\times} \mathbf{P}_n \mathbf{x} = 0
\end{array}\right.
\end{displaymath}](img1626.png) |
(9.12) |
La minimizzazione in coordinate mondo tuttavia non è ottima dal punto di vista della minimizzazione del rumore.
In mancanza di ulteriori informazioni sulla struttura della scena osservata, la stima ottima (Maximum Likelihood Estimation) è sempre quella che minimizza l'errore in coordinate immagine (reprojection) ma richiede un maggiore peso computazione e utilizzo di tecniche non lineari, in quanto la funzione di costo da minimizzare è
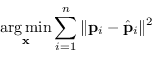 |
(9.14) |
È un problema non-lineare non-convesso: sono presenti potenzialmente vari minimi locali e la soluzione lineare deve essere usata come punto di inizio della minimizzazione.
Una ulteriore classe di tecniche, che sfruttano l'informazione ricavata dai vincoli epipolari e attraverso questa permettono di stimare la posizione dei punti non affetti da rumore senza dover ricavare il punto tridimensionale, è mostrato in sezione 9.4.4.
Paolo medici