Next: Ricostruzione tridimensionale Up: Visione Multicamera Previous: Posa relativa in coordinate
Nei capitoli precedenti è stato fatto più volte notare che da una sola immagine non è possibile ottenere le coordinate mondo dei punti che compongono l'immagine, senza informazioni addizionali.
 |
L'unica cosa che un generico punto dell'immagine ![]() può fornire, data l'equazione (8.19) della camera pin-hole, è una relazione tra le (infinite) coordinate mondo
può fornire, data l'equazione (8.19) della camera pin-hole, è una relazione tra le (infinite) coordinate mondo ![]() sottese al punto immagine ovvero il luogo delle coordinate mondo che proiettate darebbero esattamente quel particolare punto immagine.
Tale relazione è l'equazione di una retta passante per il pin-hole
sottese al punto immagine ovvero il luogo delle coordinate mondo che proiettate darebbero esattamente quel particolare punto immagine.
Tale relazione è l'equazione di una retta passante per il pin-hole ![]() e per il punto sul sensore corrispondente al punto
e per il punto sul sensore corrispondente al punto ![]() immagine.
Riportando nuovamente l'equazione (8.19), è facile vedere qual'è la dipendenza tra i parametri della camera i-esima, il punto immagine
immagine.
Riportando nuovamente l'equazione (8.19), è facile vedere qual'è la dipendenza tra i parametri della camera i-esima, il punto immagine ![]() e la retta che rappresenta tutti i possibili punti mondo
e la retta che rappresenta tutti i possibili punti mondo ![]() sottesi a
sottesi a ![]() :
:
Nel caso della visione stereo abbiamo due sensori e pertanto dobbiamo definire due sistemi di riferimento con parametri
![]() e
e
![]() rispettivi e posizione dei pin-hole
rispettivi e posizione dei pin-hole ![]() e
e ![]() espressi sempre in coordinate mondo.
espressi sempre in coordinate mondo.
La retta (9.7), luogo dei punti mondo associabili al punto immagine ![]() visto nel primo sistema di riferimento, può essere proiettata nella vista della seconda camera:
visto nel primo sistema di riferimento, può essere proiettata nella vista della seconda camera:
Questo punto costante è l'epipolo. L'epipolo è il punto di intersezione di tutte le linee epipolari e rappresenta la proiezione del pin-hole di una camera nell'immagine dell'altra ovvero il “punto di fuga” delle linee epipolari.
Date due camere le proiezioni delle coordinate dei pin-hole ![]() e
e ![]() sull'opposta immagine sono
sull'opposta immagine sono
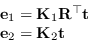 |
(9.10) |
La matrice ![]() , per costruzione, converte da coordinate camera 1 a coordinate camera 2 e
, per costruzione, converte da coordinate camera 1 a coordinate camera 2 e ![]() rappresenta la posizione del pin-hole della camera 1 espresso nel sistema di riferimento della camera 2.
rappresenta la posizione del pin-hole della camera 1 espresso nel sistema di riferimento della camera 2.
Le rette generate dai punti della prima immagine passano tutte per uno stesso punto formato dalla proiezione del pin-hole ![]() sulla seconda immagine:
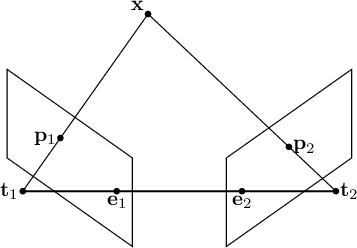
di fatto il punto in coordinate mondo e i due epipoli creano un piano (il piano epipolare) dove vivono le possibili soluzioni, i punti in coordinate camera, del problema della ricostruzione tridimensionale (figura 9.1).
sulla seconda immagine:
di fatto il punto in coordinate mondo e i due epipoli creano un piano (il piano epipolare) dove vivono le possibili soluzioni, i punti in coordinate camera, del problema della ricostruzione tridimensionale (figura 9.1).
La geometria epipolare è la geometria che lega due immagini acquisite da due punti di vista differenti. Le relazioni che intercorrono tra le immagini tuttavia non dipendono dalla scena osservata ma dipendono solamente dai parametri intrinseci delle camere e dalle pose relative.
Per ogni punto osservato, il piano epipolare è il piano formato dal punto in coordinate mondo e dai 2 centri ottici.
La linea epipolare è l'intersezione tra il piano epipolare e il piano immagine nella seconda immagine. Di fatto il piano epipolare interseca in entrambe le immagini il piano nelle rette epipolari e definisce le corrispondenze tra le linee.
Nelle prossime sezioni verrà discusso sia come ricavare la retta lungo la quale un punto appartenente ad una immagine deve trovarsi in un'altra immagine, sia come dati due (o più) punti omologhi ottenere il punto tridimensionale corrispondente.
Paolo medici