Next: Il piano epipolare Up: Trasformazione di coordinate camera Previous: Trasformazione di coordinate camera
Come già ricordato più volte, per trasformare un sistema di riferimento camera in uno sensore è sufficiente applicare la trasformazione
| (9.5) |
Per esempio, attraverso queste relazioni, è possibile ottenere le relazioni che legano le pose relative espresse in coordinate camera con quelle espresse in coordinate sensore di equazione (1.66):
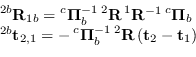 |
(9.6) |
Queste relazioni permettono di ottenere i parametri della posa relativa
![]() partendo dai parametri della camera pin-hole, relazioni che permettono di convertire coordinate sensore 1 nelle coordinate sensore 2 come in equazione 1.64.
partendo dai parametri della camera pin-hole, relazioni che permettono di convertire coordinate sensore 1 nelle coordinate sensore 2 come in equazione 1.64.
Paolo medici