Next: Rimozione rumore sotto vincoli Up: Matrice Essenziale e matrice Previous: Fattorizzazione della Matrice Essenziale
Dalla decomposizione della matrice Essenziale, a meno di un fattore moltiplicativo, esistono pertanto 4 possibili configurazioni (le due matrici di rotazione e gli associati vettori di traslazione) che ricombinate permettono di ottenere nuovamente la matrice Essenziale di origine.
Per determinare quale decomposizione è quella corretta l'unico modo è trovare la configurazione che ricostruisce la maggioranza dei punti tridimensionali in maniera opportuna ovvero, più semplicemente, la configurazione che porta la maggioranza dei punti ad avere la coordinata camera ![]() ad essere positiva.
ad essere positiva.
Sia
![]() una decomposizione della matrice Essenziale, siano
una decomposizione della matrice Essenziale, siano ![]() ,
, ![]() le coordinate camera di due punti omologhi, e si definiscano
le coordinate camera di due punti omologhi, e si definiscano
![]() e
e
![]() tali che
tali che
| (9.75) |
L'obiettivo è quello di ricavare le coordinate ![]() e
e ![]() attraverso le quali, valutandone la positività, si può supporre che i punti omologhi siano frontali rispetto all'osservatore e da questo dedurre la correttezza della decomposizione della matrice Essenziale.
Sfruttando il formalismo (9.74), l'equazione (9.38) diventa
attraverso le quali, valutandone la positività, si può supporre che i punti omologhi siano frontali rispetto all'osservatore e da questo dedurre la correttezza della decomposizione della matrice Essenziale.
Sfruttando il formalismo (9.74), l'equazione (9.38) diventa
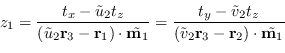 |
(9.77) |
| (9.78) |
È da notare che la soluzione del problema si poteva ottenere risolvendo direttamente il sistema (9.76) come se fosse un sistema lineare sovradimensionato di 2 incognite in 3 equazioni (approccio simile a quello che si è visto in sezione 9.3.1).
In entrambi i casi viene ottimizzata una quantità algebrica e pertanto non sarà la stima alla massima verosimiglianza del punto tridimensionale: diversamente dagli algoritmi discussi in sezione 9.3.1, questo è un approccio in effetti poco adatto per ricavare le coordinate mondo precise ma sufficiente per verificare che la scelta della decomposizione sia quella corretta.
Va sempre ricordato che essendo il vettore ![]() estratto dalla matrice Essenziale conosciuto a meno di un fattore moltiplicativo i punti così stimati sono conosciuti a meno di un fattore moltiplicativo.
estratto dalla matrice Essenziale conosciuto a meno di un fattore moltiplicativo i punti così stimati sono conosciuti a meno di un fattore moltiplicativo.
É da notare che questo discorso è chiaramente generico e può essere applicato al caso di ricostruzione tridimensionale conoscendo la posa relativa tra sensori.
Paolo medici