Next: Chiralità e ricostruzione con Up: Matrice Essenziale e matrice Previous: Stima alla Massima Verosimiglianza
Nelle sezioni precedenti si è visto come, sfruttando almeno 5 corrispondenze tra punti omologhi tra due immagini, è possibile ottenere la matrice Essenziale che codifica la posa relativa tra le due camere. La matrice Essenziale può essere nuovamente fattorizzata in rotazione e traslazione. In questo modo è possibile ottenere i parametri relativi delle camere coinvolte e, attraverso questa informazione, riuscire ad eseguire una ricostruzione tridimensionale della scena osservata.
Come suggerito da Trivedi, dalla definizione di matrice essenziale (9.41) è facile mostrare che la matrice simmetrica
![]() è indipendente dal vettore rotazione:
è indipendente dal vettore rotazione:
![\begin{displaymath}
\mathbf{E} \mathbf{E}^{\top} = [\mathbf{t}]_{\times} [\math...
...z \\
- t_z t_x & - t_z t_y & t^2_x + t^2_y \\
\end{bmatrix}\end{displaymath}](img1769.png) |
(9.71) |
La matrice Essenziale può essere anche fattorizzata direttamente attraverso la Decomposizione a Valori Singolari.
Sia
![]() , dove
, dove
![]() , la SVD di
, la SVD di ![]() (se così non fosse, è comunque possibile proiettare la matrice
(se così non fosse, è comunque possibile proiettare la matrice ![]() nello
spazio delle matrici Essenziali, come descritto in sezione 9.4.1).
Attraverso questa decomposizione si possono estrarre i componenti generatori di
nello
spazio delle matrici Essenziali, come descritto in sezione 9.4.1).
Attraverso questa decomposizione si possono estrarre i componenti generatori di ![]() :
:
| (9.72) |
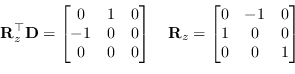 |
(9.73) |
La matrice di rotazione ![]() presenta così due possibili soluzioni ruotate di 180^ tra loro rispetto all'asse che congiunge i due pin-hole.
Siccome il vettore
presenta così due possibili soluzioni ruotate di 180^ tra loro rispetto all'asse che congiunge i due pin-hole.
Siccome il vettore ![]() è conosciuto a meno di un fattore moltiplicativo e il vincolo
è conosciuto a meno di un fattore moltiplicativo e il vincolo
![]() non permette di ricavare il segno della traslazione, esistono anche due ulteriori alternative per la fattorizzazione dovute a una ambiguità sul segno che può assumere
non permette di ricavare il segno della traslazione, esistono anche due ulteriori alternative per la fattorizzazione dovute a una ambiguità sul segno che può assumere ![]() .
Esistono pertanto 4 differenti fattorizzazioni, tutte plausibili, di una matrice Essenziale e fra queste va scelta quella che proietta tutti i punti (o la maggior parte) frontalmente rispetto ad entrambe le camere.
.
Esistono pertanto 4 differenti fattorizzazioni, tutte plausibili, di una matrice Essenziale e fra queste va scelta quella che proietta tutti i punti (o la maggior parte) frontalmente rispetto ad entrambe le camere.
Paolo medici