Next: Fattorizzazione della Matrice Essenziale Up: Matrice Essenziale e matrice Previous: Determinazione delle matrici
Quando si usa la decomposizione SVD per irrobustirne i vincoli, la matrice Fondamentale (o Essenziale) che si ottiene soddisfa pienamente i requisiti per essere Fondamentale (o Essenziale) ma tuttavia è solo una matrice più simile sotto una particolare norma (in questo caso Frobenius) a quella ottenuta dal sistema lineare. Neanche questa soluzione pertanto è ottima perchxE9 non tiene comunque conto di come avviene la propagazione dell'errore dai punti in ingresso all'interno della trasformazione: è di fatto ancora una soluzione algebrica e non geometrica.
Una prima tecnica, che minimizza l'errore geometrico, consiste nel sfruttare la distanza tra i punti e le rette epipolari generate attraverso la matrice Fondamentale (epipolar distance).
Anche solo intuitivamente, la distanza tra un punto ![]() e la retta epipolare
e la retta epipolare
![]() può essere usata come metrica per stimare l'errore geometrico:
può essere usata come metrica per stimare l'errore geometrico:
Siccome è possibile calcolare sia per la prima immagine che per la seconda questo errore, è corretto minimizzare entrambi i contributi insieme.
Attraverso questa metrica è possibile definire una funzione costo che minimizzi l'errore in maniera simmetrica (symmetric transfer error) tra le due immagini:
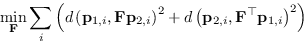 |
(9.64) |
Alternativamente al Symmetric Transfer Error in letteratura viene spesso usata l'approssimazione al primo grado della distanza tra i punti e la funzione (Sampson-error, sezione 3.3.7).
È possibile definire così una distanza approssimata tra i punti immagine omologhi
![]() e la varietà
e la varietà
![]() attraverso la metrica
attraverso la metrica
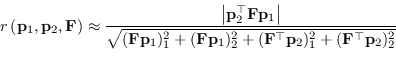 |
(9.65) |
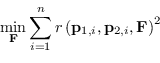 |
(9.66) |
Sia il Symmetric Transfer Error che la distanza di Sampson, metriche comunque migliori della stima algebrica, non sono lo stimatore ottimo.
La stima di massima verosimiglianza Maximum Likelihood Estimation per la matrice Fondamentale si otterrebbe infatti usando una funzione costo del tipo
Per risolvere questo problema bisogna unire il problema del calcolo della matrice Essenziale o Fondamentale con quello della ricostruzione tridimensionale e porre come variabile ausiliaria direttamente la coordinata tridimensionale del punto osservato
![]() .
.
La matrice Essenziale può essere ottenuta data la conoscenza dei parametri intrinseci dei due sensori.
In questo caso infatti è possibile sfruttare il sistema non lineare che proietta la variabile ausiliaria
![]() sulle rispettive due osservazioni sui due rispettivi sensori:
sulle rispettive due osservazioni sui due rispettivi sensori:
Quando i parametri intrinseci non sono disponibili, nel caso della stima della matrice Fondamentale, non è possibile effettuare una vera ricostruzione tridimensionale della scena proprio per la mancanza di questi parametri.
È possibile sfruttare tuttavia delle proiezioni prospettiche fittizie ponendo
![]() e ottenendo dei vincoli del tipo:
e ottenendo dei vincoli del tipo:
Inserendo i vincoli (9.70) nell'equazione (9.67) anche questa volta l'obiettivo di ricavare la matrice Fondamentale viene trasformato in quello di ricavare i parametri della matrice proiettiva ![]() .
Attraverso la matrice camera
.
Attraverso la matrice camera
![]() , matrice camera fittizia, è infine possibile ricavare
, matrice camera fittizia, è infine possibile ricavare ![]() applicando direttamente la definizione (9.41) dove tuttavia la matrice
applicando direttamente la definizione (9.41) dove tuttavia la matrice ![]() non è una matrice di rotazione.
non è una matrice di rotazione.
La stima a massima Verosimiglianza della matrice Fondamentale, corretta dal punto di vista probabilistico, richiede comunque una gran quantità di risorse: oltre alle 12 incognite globali necessarie per stimare ![]() (rispetto alle 5 della matrice Essenziale) per ogni coppia di punti da minimizzare vengono inserite nel problema 3 ulteriori incognite.
(rispetto alle 5 della matrice Essenziale) per ogni coppia di punti da minimizzare vengono inserite nel problema 3 ulteriori incognite.
Infine, come avvertenza finale, per la stima ottima delle matrici in presenza di eventuali outlier nella scena sono ampiamente sfruttate tecniche come RANSAC (sezione 3.12).
Paolo medici