Next: Punti omologhi in spazi Up: Visione Multicamera Previous: Chiralità e ricostruzione con
Come si è visto in sezione 9.3.1, triangolare punti affetti da rumore porta a rette non incidenti la cui intersezione non minimizza il residuo in coordinate immagine (per esempio sotto la metrica della distanza euclidea). Abbiamo anche visto che la miglior stima dei punti non affetti da rumore minimizza la quantità di equazione 9.67 sotto il vincolo epipolare 9.68. Finora però, data la conoscenza della matrice Essenziale/Fondamentale, questa minimizzazione ha richiesto il punto tridimensionale come variabile ausiliaria e una tecnica (iterativa) di ottimizzazione inizializzata per esempio sfruttando la triangolazione con rette sghembe dei punti affetti da rumore.
Esiste una tecnica globale non lineare che permette di ottenere la triangolazione ottima (la stima dei punti immagine) attraverso un metodo polinomiale (HS97) che richiede di trovare le radici di un polinomio di 6^ grado.
Come più chiaramente discusso in (Lin10), la triangolazione ottima può essere vista come il seguente problema di minimizzazione:
| (9.79) |
| (9.80) |
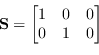 |
(9.81) |
Questo problema di minimizzazione vincolata si può risolvere attraverso l'ausilio dei moltiplicatori di Lagrange:
| (9.82) |
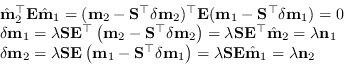 |
(9.83) |
Sempre in (Lin10) vengono proposte anche tecniche sub-ottime, iterative, dal basso costo computazionale, dove ad ogni iterazione il vincolo epipolare viene comunque soddisfatto.
Ottenuti i punti immagine non affetti da rumore, con qualsiasi tecnica di triangolazione (rette sghembe di sezione 1.5.6 o la DLT di sezione 9.3.1) è possibile ricavare il punto tridimensionale.
Una formulazione alternativa (KK95), dati due punti omologhi espressi in coordinate camera
![]() e
e
![]() il punto tridimensionale formato dall'intersezione dei raggi ottici è
il punto tridimensionale formato dall'intersezione dei raggi ottici è
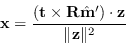 |
(9.84) |
Paolo medici