Next: Retta in coordinante polari Up: Linee, Piani e Iperpiani Previous: Principio di Dualità
Nello spazio ![]() , e in generale in tutti gli spazi di dimensione superiore, due rette
, e in generale in tutti gli spazi di dimensione superiore, due rette ![]() e
e ![]() possono non incrociarsi in nessun punto anche se non sono parallele.
Tali rette si definiscono sghembe (skew lines).
Per queste particolari rette un parametro di interesse è la loro distanza minima e, conseguentemente, i punti sulle due rette che rappresentano tale minimo.
possono non incrociarsi in nessun punto anche se non sono parallele.
Tali rette si definiscono sghembe (skew lines).
Per queste particolari rette un parametro di interesse è la loro distanza minima e, conseguentemente, i punti sulle due rette che rappresentano tale minimo.
Siano due rette formate da punti ![]() e
e ![]() di equazione
di equazione
La “distanza” tra due generici punti sulle due rette è
| (1.42) |
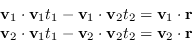 |
(1.43) |
Esiste anche una formulazione alternativa al risolvere il sistema lineare giungendo allo stesso risultato attraverso considerazioni puramente geometriche.
Si può dimostrare che la distanza tra le due rette in ![]() vale
vale
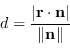 |
(1.44) |
Il piano formato dalla traslazione della seconda retta lungo ![]() interseca la prima retta nel punto di minima distanza
interseca la prima retta nel punto di minima distanza
 |
(1.45) |
Indipendentemente dal formalismo scelto, mettendo questi valori dentro le equazioni 1.41 si ricavano le coordinate tridimensionali dei punti tra loro più vicini delle rette.
Paolo medici