Next: Matrice Essenziale e matrice Up: Ricostruzione tridimensionale Previous: Ricostruzione tridimensionale e omografia
Esaminiamo il caso particolare in cui le camere sono allineate rispetto agli assi, hanno parametri intrinseci uguali, rotazione relativa nulla e siano inclinate dell'angolo di beccheggio pitch rispetto al piano ![]() .
.
In questa particolare condizione la matrice di proiezione si semplifica leggermente assumendo la forma
La coordinata orizzontale ![]() di un generico punto
di un generico punto ![]() in coordinate mondo vale di conseguenza:
in coordinate mondo vale di conseguenza:
Con le ipotesi di camere rettificate viste in precedenza, ovvero stessa orientazione e parametri intrinseci uguali, condizione che si può sempre ottenere con la rettificazione o considerando righe opportune dell'immagine,
la matrice proiettiva (9.25) risulta essere la stessa nei due sistemi di riferimento differenti e, osservando l'equazione (9.26), l'unica differenza tra camere differenti risulta essere il solo numeratore a causa della differente posizione del pin-hole lungo l'asse delle ![]() .
Ne consegue che la differenza delle coordinate
.
Ne consegue che la differenza delle coordinate ![]() nelle due immagini
nelle due immagini ![]() (disparità) vale
(disparità) vale
| (9.28) |
| (9.29) |
La coordinata ![]() del punto si può scrivere invece come
del punto si può scrivere invece come
Da cui il sistema di equazioni:
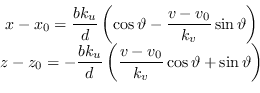 |
(9.32) |
Un caso particolare di disparità è quando si osserva un piano, quello del terreno, che, per numero di punti, è preponderante sull'immagine.
Nel caso in cui la baseline sia lungo l'asse ![]() , la disparità del piano
, la disparità del piano ![]() è solo funzione di
è solo funzione di ![]() e tale equazione risulta essere quella di una retta.
e tale equazione risulta essere quella di una retta.
La relazione della disparità dalla coordinata ![]() si può ricavare dal valore di
si può ricavare dal valore di ![]() dalla seconda e sostituendolo nella prima delle equazioni (9.31):
dalla seconda e sostituendolo nella prima delle equazioni (9.31):
Dalla prima delle equazioni (9.33), si vede che l'espressione della disparità dipende solamente dalla distanza ![]() se l'altezza
se l'altezza ![]() è fissata (ad esempio sul suolo),
e dalla seconda si vede che la disparità
è fissata (ad esempio sul suolo),
e dalla seconda si vede che la disparità ![]() cresce linearmente con la coordinata
cresce linearmente con la coordinata ![]() seguendo un coefficiente angolare noto
seguendo un coefficiente angolare noto
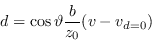 |
(9.34) |
| (9.35) |
Paolo medici