Next: Camere inclinate rispetto a Up: Ricostruzione tridimensionale Previous: Camere allineate e triangolazione
L'equazione (9.21) è facilmente esprimibile in forma omogenea.
La matrice che permette dalle coordinate immagine-disparità di ricostruire direttamente le coordinate del punto tridimensionale espresso nel sistema di riferimento camera è
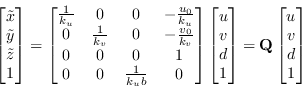 |
(9.22) |
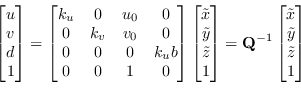 |
(9.23) |
In condizioni reali, essendo la camera rototraslata rispetto alle condizioni ideali, è sufficiente moltiplicare la matrice ![]() per la matrice
per la matrice ![]() , rappresentante la trasformazione tra coordinate camera a mondo, per ottenere una nuova matrice che permette di passare da coordinate disparità a coordinate mondo e viceversa.
, rappresentante la trasformazione tra coordinate camera a mondo, per ottenere una nuova matrice che permette di passare da coordinate disparità a coordinate mondo e viceversa.
L'utilizzo di tale formalismo permette di trasformare punti disparità acquisiti da coppie di camere posizionate in punti di vista differenti (ad esempio una coppia stereo che si sposta nel tempo o due coppie stereo rigidamente connesse tra loro).
In questo caso la relazione che lega punti disparità acquisiti nei due punti di vista è anche rappresentata da una matrice ![]() :
:
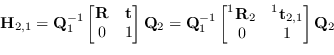 |
(9.24) |
Paolo medici