Next: Camere allineate e triangolazione Up: Ricostruzione tridimensionale Previous: Ricostruzione con camere rettificate
Nel caso di camere perfettamente allineate rispetto agli assi e aventi parametri intrinseci uguali (stessa focale e stesso principal point) le equazioni per la ricostruzione tridimensionale si semplificano enormemente.
In questa condizione le equazioni della proiezione prospettica si riducono a
Limitiamoci ora al solo caso stereoscopico: per semplicità verrà indicato con il pedice 1 la camera sinistra e 2 la camera destra.
I vincoli di allineamento impongono ![]() ,
, ![]() ,
, ![]() e
e ![]() avendo posto, senza perdita di generalità, la camera destra al centro del sistema di riferimento.
La quantità
avendo posto, senza perdita di generalità, la camera destra al centro del sistema di riferimento.
La quantità ![]() è definita baseline.
è definita baseline.
La differenza ![]() delle coordinate orizzontali delle proiezioni un medesimo punto visto nelle due immagini della coppia stereo si definisce disparità.
Tale valore si ottiene inserendo i vincoli di allineamento nell'equazione (9.15) e risulta
delle coordinate orizzontali delle proiezioni un medesimo punto visto nelle due immagini della coppia stereo si definisce disparità.
Tale valore si ottiene inserendo i vincoli di allineamento nell'equazione (9.15) e risulta
Invertendo questa semplice relazione e sostituendola in equazione (9.15) è possibile ricavare il punto in coordinate mondo ![]() corrispondente a un punto
corrispondente a un punto ![]() della camera destra con disparità
della camera destra con disparità ![]() :
:
Come è possibile notare, ogni elemento è determinato attraverso il fattore moltiplicativo ![]() della baseline, vero fattore di scala della ricostruzione, e dall'inverso della disparità
della baseline, vero fattore di scala della ricostruzione, e dall'inverso della disparità ![]() .
.
Le coordinate ![]() così ottenute sono coordinate sensore, riferite a una configurazione stereoscopica particolare dove orientazione e posizionamento sono allineati e coincidenti con gli assi del sistema.
Per passare da coordinate sensore al caso generico di coordinate mondo, con camere arbitrariamente orientate, bisogna applicare una trasformazione che porti le coordinate da sensore a mondo, ovvero la matrice di rotazione
così ottenute sono coordinate sensore, riferite a una configurazione stereoscopica particolare dove orientazione e posizionamento sono allineati e coincidenti con gli assi del sistema.
Per passare da coordinate sensore al caso generico di coordinate mondo, con camere arbitrariamente orientate, bisogna applicare una trasformazione che porti le coordinate da sensore a mondo, ovvero la matrice di rotazione
![]() e la traslazione
e la traslazione
![]() coordinata del pin-hole, in modo da poter scrivere
coordinata del pin-hole, in modo da poter scrivere
Unendo l'equazione (9.17) con l'equazione (9.18), è possibile definire una matrice ![]() in modo che la conversione tra punto immagine-disparità
in modo che la conversione tra punto immagine-disparità ![]() e coordinata mondo
e coordinata mondo ![]() si possa scrivere in forma molto compatta come
si possa scrivere in forma molto compatta come
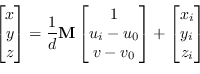 |
(9.19) |
Paolo medici