Next: La divisione del piano Up: Linee, Piani e Iperpiani Previous: Retta in coordinante polari
È possibile generalizzare il discorso delle rette a piani ed iperpiani nello spazio
![]() .
Come per le rette infatti esiste una forma implicita e omogenea dell'equazione di un piano intesa come luogo dei punti espressi dalla coordinata
.
Come per le rette infatti esiste una forma implicita e omogenea dell'equazione di un piano intesa come luogo dei punti espressi dalla coordinata
![]() omogenea a
omogenea a
![]() :
:
| (1.48) |
Le coordinate omogenee sono conosciute a meno di un fattore moltiplicativo e pertanto si può forzare un vincolo opzionale: come per le rette si può pensare che i primi ![]() parametri della coordinata omogenea formino un vettore di lunghezza unitaria.
parametri della coordinata omogenea formino un vettore di lunghezza unitaria.
Un generico piano, o iperpiano, è dunque il luogo dei punti
![]() che soddisfano la condizione
che soddisfano la condizione
Bisogna ricordare che i gradi di libertà sono comunque sempre e solo ![]() .
.
Quando introdotto, il vincolo di normalizzazione
![]() rappresenta un caso particolare: sotto questa condizione, come nel caso delle rette,
rappresenta un caso particolare: sotto questa condizione, come nel caso delle rette, ![]() assume il significato di minima distanza euclidea tra il piano e l'origine.
assume il significato di minima distanza euclidea tra il piano e l'origine.
Se il piano (o l'iperpiano) è normalizzato, la distanza tra un generico punto ![]() e il piano si misura come
e il piano si misura come
Il punto ![]() più vicino a un generico punto
più vicino a un generico punto ![]() appartenente all'iperpiano si trova nell'intersezione tra la retta di direzione
appartenente all'iperpiano si trova nell'intersezione tra la retta di direzione ![]() passante per
passante per ![]() e il piano stesso:
e il piano stesso:
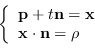 |
(1.53) |
Per quanto riguarda i vari metodi per la generazione, nella sezione 3.6.3 verrà mostrato come ottenere la regressione ai minimi quadrati di un insieme di punti all'equazione di piano.
Come nel caso della retta, anche i parametri del piano in ![]() possono essere espressi attraverso l'uso di 3 coordinate polari (azimuth, zenith e
possono essere espressi attraverso l'uso di 3 coordinate polari (azimuth, zenith e ![]() ):
):
Paolo medici