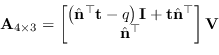Si sono viste nelle sezioni precedenti esempi di prospettiva inversa: la possibilità di ricavare il punto 3D dato un punto immagine 2D e la conoscenza di un vincolo nel mondo sulla cui superficie il punto giace.
É sempre possibile infatti creare un sistema tra il raggio ottico (8.19) è una varietà in 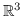 :
:
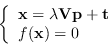 |
(8.41) |
avendo chiamato
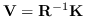 .
Questa stessa formulazione si usa in grafica computazionale per indicare le tecniche di RayTracing.
Generalizziamo in questa sezione diverse casistiche.
.
Questa stessa formulazione si usa in grafica computazionale per indicare le tecniche di RayTracing.
Generalizziamo in questa sezione diverse casistiche.
Un generico piano in 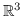 scritto nella forma
scritto nella forma
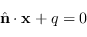 |
(8.42) |
è un vincolo per permettere l'intersezione tra il raggio ottico (8.19) e il piano (8.42).
Il sistema (8.41) è lineare e può essere risolto per 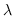 e da
e da 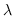 inserita nella prima equazione determinare il punto 3D.
É possibile realizzare anche una applicazione lineare associata all'intersezione piano retta nella forma
inserita nella prima equazione determinare il punto 3D.
É possibile realizzare anche una applicazione lineare associata all'intersezione piano retta nella forma
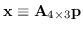 avendo definito
avendo definito
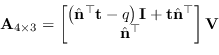 |
(8.43) |
La varietà ha equazione
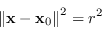 |
(8.44) |
che unita al sistema (8.41) permette di ottenere
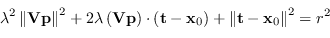 |
(8.45) |
La soluzione dell'equazione di secondo grado può pertanto avere 0 (nessuna intersezione), 1 (raggio ottico tangente alla sfera) o 2 radici (il raggio ottico interseca la sfera).
Subsections
Paolo medici
2025-03-12