Next: Rettificazione Up: Trasformazioni omografiche notevoli Previous: Vanishing Point e linea
L'equazione generica che mette in relazione i punti immagine tra due punti di vista generici si può scrivere come
In genere non è possibile trasformare una vista generata da una camera nella vista generata da un altra. Ciò risulta possibile solo se si vuole rimappare correttamente solamente i punti di un determinato piano o quando le camere condividono lo stesso pin-hole.
Il secondo caso lo vedremo nella prossima sezione.
Nel primo caso è possibile rimappare i punti da una visuale a quelli di un'altra sfruttando la combinazione di una Perspective Mapping seguita da una Inverse Perspective Mapping e sfruttando l'ipotesi che la scena osservata sia composta solamente da un piano (per esempio il suolo).
I punti immagine vengono proiettati in coordinate mondo su una camera 1 e riproiettati di nuovo in coordinate immagine su una seconda camera 2 con parametri intrinseci ed estrinseci differenti.
Siccome si riproietta sempre un piano, anche la composizione di questa trasformazione è ancora una omografia:
| (8.36) |
Dal punto di vista teorico il fatto di dover forzare un piano ![]() costante incide solamente se il vettore traslazione cambia.
Nel caso in cui il vettore di traslazione venga modificato tra le due viste ed esistano punti non appartenenti al piano indicato avviene una rimappatura errata tra le due viste (la trasformazione omografica non è più rispettata).
La trasformazione (8.35) può servire per individuare anche ostacoli verticali all'interno di tecniche come il Ground Plane Stereo e il Motion Stereo.
costante incide solamente se il vettore traslazione cambia.
Nel caso in cui il vettore di traslazione venga modificato tra le due viste ed esistano punti non appartenenti al piano indicato avviene una rimappatura errata tra le due viste (la trasformazione omografica non è più rispettata).
La trasformazione (8.35) può servire per individuare anche ostacoli verticali all'interno di tecniche come il Ground Plane Stereo e il Motion Stereo.
Questa matrice omografica si può generalizzare conoscendo gli elementi della trasformazione delle due viste
![]() e l'equazione del piano
e l'equazione del piano
![]() , dove
, dove
![]() è la normale al piano e
è la normale al piano e ![]() è la distanza tra la prima camera con il piano stesso. In questo caso infatti, un punto
è la distanza tra la prima camera con il piano stesso. In questo caso infatti, un punto ![]() della prima vista appartenente al piano soddisfa l'equazione
della prima vista appartenente al piano soddisfa l'equazione
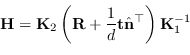 |
(8.39) |
Paolo medici