Next: Trasformazioni tra immagini e Up: Elementi Previous: Omografia e Coniche
Si consideri il problema di verificare se un punto è all'interno di poligoni relativamente semplici come i triangoli o i quadrilateri. La trattazione del caso di poligono generico è più complessa e viene lasciata al lettore (e opzionalmente riconducibile al caso triangolo/quadrilatero).
Nel caso di triangoli e quadrilateri gli approcci che saranno mostrati risultano molto efficienti nel caso in cui sia necessario eseguire confronti tra un singolo poligono verso un numero elevato di punti in quanto tali tecniche permettono l'utilizzo di precalcoli: l'idea base infatti è quella di sfruttare una trasformazione dello spazio delle coordinate del poligono in uno spazio dove risulti più facile eseguire il confronto.
Per esempio, un parallelogramma formato da due vettori generatori può sempre essere trasformato in un quadrato unitario ![]() attraverso una trasformazione affine
attraverso una trasformazione affine
![]() .
Un punto
.
Un punto ![]() cade all'interno del parallelogramma se
cade all'interno del parallelogramma se
![]() e
e
![]() .
La stessa trasformazione vale anche per i triangoli formati dagli stessi vettori generatori, con però il confronto
.
La stessa trasformazione vale anche per i triangoli formati dagli stessi vettori generatori, con però il confronto
![]() e
e
![]() .
Per valutare se un punto cade all'interno del parallelogramma sono necessarie appena 4 moltiplicazioni e 6 somme.
Il costo di creazione della trasformazione affine è più elevato ma se il numero di confronti è alto tale peso, costante, risulta trascurabile.
.
Per valutare se un punto cade all'interno del parallelogramma sono necessarie appena 4 moltiplicazioni e 6 somme.
Il costo di creazione della trasformazione affine è più elevato ma se il numero di confronti è alto tale peso, costante, risulta trascurabile.
Per trasformare quadrilateri generici in un quadrato unitario ![]() si deve usare invece la trasformazione omografica (si veda la sezione 1.10).
A scapito di un costo iniziale elevato di creazione della trasformazione, il controllo se un punto appartiene o meno alla figura geometrica è relativamente semplice
si deve usare invece la trasformazione omografica (si veda la sezione 1.10).
A scapito di un costo iniziale elevato di creazione della trasformazione, il controllo se un punto appartiene o meno alla figura geometrica è relativamente semplice
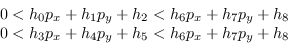 |
(1.86) |
Paolo medici