Next: Trasformazioni omografiche Up: Posa relativa tra sensori Previous: Posa relativa tra sensori
Ci sono diverse tecniche per ottenere una stima ottima della trasformazione di rotazione e traslazione rigida tra punti appartenenti al medesimo spazio.
Per stima ottima si intende la stima alla massima verosimiglianza, dove il rumore di osservazione ![]() è totalmente additivo nello spazio
è totalmente additivo nello spazio
![]() in cui vivono i punti.
in cui vivono i punti.
Siano pertanto due insiemi di punti
![]() e
e
![]() tali che siano messi in relazione da
tali che siano messi in relazione da
Per risolvere il problema ottimo
![]() che trasforma tutti i punti da
che trasforma tutti i punti da
![]() a
a
![]() è richiesto un criterio ai minimi quadrati che ottimizzi una funzione costo del tipo
è richiesto un criterio ai minimi quadrati che ottimizzi una funzione costo del tipo
Un risultato notevole che riguarda il vettore traslazione si ricava applicando le classiche derivate
![]() all'equazione (1.69) che si annulla in
all'equazione (1.69) che si annulla in
| (1.70) |
La rotazione ![]() ottima deve minimizzare pertanto
ottima deve minimizzare pertanto
 .
Pertanto qualunque problema di registrazione di pose in
.
Pertanto qualunque problema di registrazione di pose in
Una prima tecnica per calcolare la rotazione fa uso delle componenti principali (si veda sezione 2.10.1).
Le componenti principali estratte da ogni insieme di punti separatamente sono una base dello spazio. È possibile determinare una rotazione che le fa combaciare tali basi in quanto ricavate le matrici degli autovettori colonna ![]() e
e ![]() si ottiene direttamente
si ottiene direttamente
![]() .
Possono esistere tuttavia più soluzioni (e ognuna andrebbe verificata) e a causa del rumore ricavare gli assi attraverso PCA può diventare estremamente inaffidabile (ad esempio se la distribuzione risultasse circolare risulterebbe impossibile qualsiasi stima).
.
Possono esistere tuttavia più soluzioni (e ognuna andrebbe verificata) e a causa del rumore ricavare gli assi attraverso PCA può diventare estremamente inaffidabile (ad esempio se la distribuzione risultasse circolare risulterebbe impossibile qualsiasi stima).
La cosa migliore per minimizzare (1.71) consiste nel minimizzare o meglio massimizzare:
 |
(1.72) |
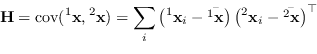 |
(1.73) |
| (1.74) |
Questa soluzione, molto più stabile di quella basata su PCA e sempre valida per ![]() , richiede una attenzione particolare nei soli casi bidimensionali e tridimensionali per gestire eventuali riflessioni (in tal caso infatti il determinante della matrice risultante potrebbe risultare negativo).
, richiede una attenzione particolare nei soli casi bidimensionali e tridimensionali per gestire eventuali riflessioni (in tal caso infatti il determinante della matrice risultante potrebbe risultare negativo).
Lo “svantaggio” della tecnica basata su SVD rispetto a quella basata su PCA è la richiesta che le associazioni tra i punti delle due distribuzioni siano corrette.
L'unione delle due tecniche insieme ad un approccio iterativo prende il nome di Iterative Closest Point (ICP).
Paolo medici