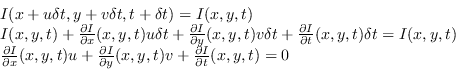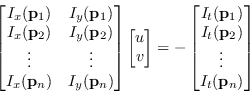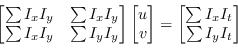Lucas-Kanade
Il metodo di stima del flusso ottico di Lucas-Kanade (LK81) è un metodo per stimare il movimento di caratteristiche interessanti in scene successive di un video.
L'obiettivo è quello di associare un vettore movimento 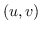 ad ogni pixel “interessante” della scena confrontando due immagini consecutive.
ad ogni pixel “interessante” della scena confrontando due immagini consecutive.
L'algoritmo fa le seguenti assunzioni:
- La luminosità tra immagini consecutive non cambia;
- Le due immagini devono essere temporalmente vicine in maniera che gli oggetti non abbiano uno scostamento significativo (l'algoritmo lavora bene con oggetti in lento movimento);
- L'immagine contiene oggetti con sufficiente tessitura in scala di grigi (l'algoritmo originale non usa esplicitamente il colore) il cui gradiente cambia graduatamente.
Partendo dell'equazione del flusso ottico per ogni punto 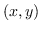 :
:
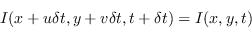 |
(7.2) |
dove 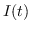 è un immagine e
è un immagine e
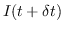 la consecutiva.
Con l'espansione in serie di taylor al primo ordine:
la consecutiva.
Con l'espansione in serie di taylor al primo ordine:
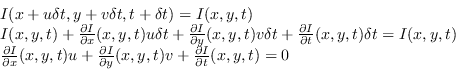 |
(7.3) |
L'algoritmo di Lucas-Kanade assume che il cambiamento di luminosità di un pixel della scena venga totalmente compensato dal gradiente della scena stessa ovvero
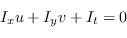 |
(7.4) |
dato il gradiente temporale 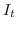 e il gradiente spaziale
e il gradiente spaziale 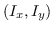 .
.
Ovviamente il singolo pixel non contiene abbastanza informazione per risolvere questo problema.
Per raccogliere più osservazioni viene assunto che un intorno del pixel abbbia lo stesso moto, ovvero
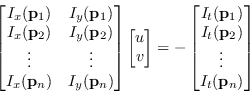 |
(7.5) |
dove
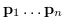 sono i punti nell'intorno del punto da stimare.
La soluzione può essere ottenuta attraverso il metodo delle normal equations
sono i punti nell'intorno del punto da stimare.
La soluzione può essere ottenuta attraverso il metodo delle normal equations
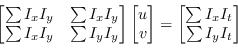 |
(7.6) |
Se si nota questa è anche la matrice dei punti caratteristici sfruttata poi da Shi-Tomasi o da Harris (vedi 5.2): i punti caratteristici di questa matrice sono punti che vengono facilmente tracciati con l'algoritmo di Lucas-Kanade.
Quando il moto è più grande di un pixel è necessario un algoritmo iterativo per risolvere il problema e un approccio coarse-to-fine per evitare i minimi locali: esisterà una scala per la quale il moto del pixel sarà inferiore ad un pixel.
Paolo medici
2025-03-12
![]() ad ogni pixel “interessante” della scena confrontando due immagini consecutive.
ad ogni pixel “interessante” della scena confrontando due immagini consecutive.
![]() :
: