Next: Elementi di Statistica Up: Elementi Previous: Minimi, Massimi e Punti
Sia ![]() una generica immagine a toni di grigio.
Il valore del pixel
una generica immagine a toni di grigio.
Il valore del pixel ![]() dell'immagine integrale
dell'immagine integrale ![]() rappresenta la somma dei valori di ogni pixel dell'immagine sorgente contenuti all'interno del rettangolo
rappresenta la somma dei valori di ogni pixel dell'immagine sorgente contenuti all'interno del rettangolo ![]() :
:
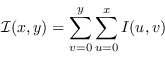 |
(1.99) |
L'artificio computazione di usare l'immagine integrale permette di ottimizzare diversi algoritmi mostrati in questo libro in particolare SURF (sezione 5.4) e l'estrazione delle feature di Haar (sezione 6.1).
Grazie all'immagine integrale è possibile, ad un costo computazionale costante di 4 somme, ottenere la sommatoria di una qualunque sottoparte rettangolare dell'immagine ![]() :
:
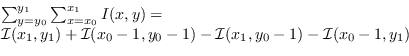 |
(1.100) |
Il valore cosı ottenuto rappresenta la somma degli elementi dell'immagine originale all'interno del rettangolo (estremi inclusi).
Oltre a poter calcolare velocemente la sommatoria di una qualsiasi sottoparte dell'immagine, è possibile ottenere facilmente convoluzioni con kernel di forma particolare in maniera molto agevole e sempre con prestazioni invarianti rispetto alla dimensione del filtro. Esempi di maschere di convoluzione si possono vedere in sezione 6.1.
Paolo medici