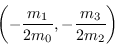Minimi e Massimi in più dimensioni

In due dimensioni, ma lo stesso discorso vale per qualunque dimensione, bisogna estendere il problema di ricerca del massimo a funzioni via via sempre più complesse.

La soluzione più immediata è analizzare il punto lungo ogni direzione spaziale in maniera indipendente: in questo modo il problema si riconduce totalmente al caso monodimensionale.

Se si vuole sfruttare invece un intorno più ampio, il successivo modello più semplice da utilizzare è il paraboloide, quadrica scritta nella forma

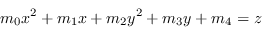$$m_0 x^2 + m_1 x + m_2 y^2 + m_3 y + m_4 = z$$ (1.94)

dove i punti 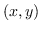$(x,y)$ sono sempre da intendersi come scostamenti rispetto al punto da modellare e 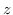$z$ è il valore che assume la funzione in quel determinato punto. Rispetto alla soluzione con gli assi totalmente separati, con questa equazione anche i punti non sugli assi contribuiscono attivamente alla soluzione del problema. Chiaramente se nel sistema si inseriscono solamente i 5 punti lungo gli assi, la soluzione sarà esattamente la stessa del caso visto nella sezione precedente.

Ogni elemento del problema fornisce pertanto un vincolo nella forma

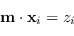$$\mathbf{m} \cdot \mathbf{x}_i=z_i$$ (1.95)

e tutti i vincoli insieme generano un sistema lineare potenzialmente sovradimensionato. In questo caso non esistono risultati notevoli con cui ottenere in forma chiusa la soluzione ma la cosa più semplice da fare è precalcolare una fattorizzazione del sistema formato dagli elementi 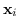$\mathbf{x}_i$, rappresentante un particolare intorno di 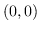$(0,0)$, in modo da velocizzare la successiva risoluzione nel momento in cui i valori 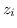$z_i$ saranno conosciuti.

L'equazione (1.94) assume gradiente nullo nel punto

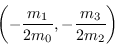$$\left( - \frac{m_1}{2 m_0}, - \frac{m_3}{2 m_2} \right)$$ (1.96)

esattamente come per il caso monodimensionale, in quanto le due componenti, quella lungo la 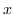$x$ e quella lungo la 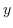$y$, rimangono comunque separate in fase di valutazione. Tale risultato è estendibile a casi n-dimensionali.