Next: Minimi e Massimi in Up: Accuratezza Sub-Pixel Previous: Accuratezza Sub-Pixel
|
|
Se il punto da esaminare è il massimo o il minimo di una sequenza monodimensionale, si può approssimare il primo vicinato del punto con una quadrica di equazione
![]() .
La quadrica è il grado di funzione minimo che permetta l'individuazione di minimi o massimi locali.
.
La quadrica è il grado di funzione minimo che permetta l'individuazione di minimi o massimi locali.
Siano pertanto ![]() ,
, ![]() e
e ![]() i valori della funzione con scostamento di
i valori della funzione con scostamento di ![]() ,
, ![]() e
e ![]() rispetto al minimo/massimo individuato con precisione del pixel.
L'equazione della quadrica passante per questi 3 punti assume la forma notevole
rispetto al minimo/massimo individuato con precisione del pixel.
L'equazione della quadrica passante per questi 3 punti assume la forma notevole
| (1.90) |
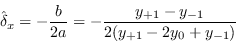 |
(1.91) |
Questa equazione fornisce anche un ulteriore risultato notevole: se ![]() è un punto di massimo/minimo locale significa che tale valore sarà, per definizione, minore/maggiore sempre sia di
è un punto di massimo/minimo locale significa che tale valore sarà, per definizione, minore/maggiore sempre sia di ![]() che di
che di ![]() .
Grazie a questa considerazione, si dimostra facilmente che
.
Grazie a questa considerazione, si dimostra facilmente che
![]() è sempre compreso tra
è sempre compreso tra ![]() e
e ![]() .
.
Esiste una formulazione alternativa: chiamando
![]() e
e
![]() l'equazione della parabola diventa
l'equazione della parabola diventa
| (1.92) |
 |
(1.93) |
Paolo medici