Omografia e Rette

Esistono applicazioni interessanti dell'omografia in diversi ambiti.

Una trasformazione omografica trasforma generalmente rette in rette. In casi particolari però può trasformare rette in punti, come ad esempio nella proiezione prospettica di elementi all'orizzonte: le coordinate omogenee infatti rappresentano diversamente punti e vettori, e quando una retta si riduce a un punto, la sua coordinata omogenea diventa 0.

La trasformazione omografica applicata a una retta (effetto del dualismo punto-retta) è esattamente la trasformazione inversa di quella che trasforma i punti corrispondenti tra gli spazi: la trasformazione $\mathbf{H}_{ij}$ che trasforma punti $\mathbf{x}_i$ dall'immagine $i$ a punti $\mathbf{x}_j$ dell'immagine $j$ trasforma equazioni delle rette dall'immagine $j$ all'immagine $i$:

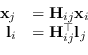$$\begin{array}{rl} \mathbf{x}_j & = \mathbf{H}_{ij} \mathbf{... ...mathbf{l}_i & = \mathbf{H}^{\top}_{ij} \mathbf{l}_j \end{array}$$ (1.82)

Esaminando punti e rette all'infinito (esempio all'orizzonte) si vede come un punto all'infinito abbia coordinate $(x,y,0)^{\top}$. Esiste pertanto una linea speciale $\mathbf{l}_{\infty}=(0,0,1)^{\top}$ che congiunge tutti questi punti.

Il principio di dualità permette di spiegare come, data una trasformazione $\mathbf{M}$ (proiettiva o omografica), la trasformazione che trasforma un punto $\mathbf {x}$ in $\mathbf{x}'$ si scriva

$$\mathbf{x}' = \mathbf{M}\mathbf{x}$$ (1.83)

mentre la trasformazione che trasforma una retta $\mathbf{l}$ diventi invece

$$\mathbf{l}' = \mathbf{M}^{-\top}\mathbf{l}$$ (1.84)