Next: Rappresentazione neurale e campi Up: Ricostruzione, rappresentazione e disegno Previous: Armoniche Sferiche
Per molti aspetti i point-based ![]() -blending, i rendering volumetrici NeRF-style e i Gaussian Splatting condividono la parte di basso livello per disegnare la scena:
il colore in un pixel dell'immagine viene approssimato integrando i campioni lungo il raggio che attraversa questo pixel. Il colore finale è una somma ponderata dei colori dei punti 3D campionati lungo questo raggio, ponderata in base alla trasmittanza.
-blending, i rendering volumetrici NeRF-style e i Gaussian Splatting condividono la parte di basso livello per disegnare la scena:
il colore in un pixel dell'immagine viene approssimato integrando i campioni lungo il raggio che attraversa questo pixel. Il colore finale è una somma ponderata dei colori dei punti 3D campionati lungo questo raggio, ponderata in base alla trasmittanza.
Il colore ![]() di un pixel è l'integrale delle varie densità che si incontrano lungo il raggio ottico
di un pixel è l'integrale delle varie densità che si incontrano lungo il raggio ottico
![]() nell'intervallo
nell'intervallo ![]() :
:
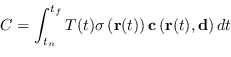 |
(9.95) |
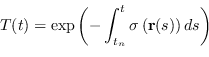 |
(9.96) |
Gli integrali possono essere trasformati in sommatorie dei vari contributi.
Il colore ![]() di un pixel può essere visto pertanto come sommatoria di vari contributi:
di un pixel può essere visto pertanto come sommatoria di vari contributi:
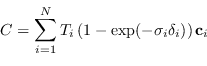 |
(9.97) |
Questa rappresentazione si riduce al classico ![]() -blending usando
-blending usando
![]() .
In questo modo anche la trasmittanza si può scrivere come
.
In questo modo anche la trasmittanza si può scrivere come
![]() .
.
Nei tipici approcci basato sui punti neurali, il colore ![]() di un pixel si ricava fondendo gli
di un pixel si ricava fondendo gli ![]() punti ordinati che sottendono il pixel stesso:
punti ordinati che sottendono il pixel stesso:
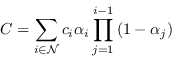 |
(9.98) |
Paolo medici