Next: Ricostruzione, rappresentazione e disegno Up: Visione Multicamera Previous: Punti omologhi in spazi
La Visual Odometry si pone come obiettivo quello di ricavare la posa relativa che ha assunto una camera (o una coppia stereoscopica) che si muove nello spazio analizzando due immagini in sequenza. Il problema dell'odometria visuale per una sola telecamera si risolve normalmente con il calcolo della matrice essenziale e la sua successiva decomposizione. In questo caso, come già indicato in precedenza, non è possibile conoscere la scala del movimento, ma solo mettere in relazione tra loro i vari movimenti. Discorso differente nel caso in cui si ha a disposizione una coppia stereoscopica.
Data una serie di osservazioni temporali di punti mondo ricavati dalla ricostruzione tridimensionale
![]() è possibile ricavare in maniera lineare una trasformazione di rototraslazione
è possibile ricavare in maniera lineare una trasformazione di rototraslazione
![]() che trasforma i punti del mondo all'istante di tempo
che trasforma i punti del mondo all'istante di tempo ![]() all'istante di tempo
all'istante di tempo ![]() in modo da poter essere espressi con una equazione del tipo:
in modo da poter essere espressi con una equazione del tipo:
La rototraslazione eseguita dalla coppia di sensori può essere ricavata minimizzando la quantità:
L'approccio mostrato ora è generale ma mal si adatta al caso di punti mondo ottenuti da una ricostruzione tridimensionale da immagini.
La funzione costo mostrata, infatti, ottimizza quantità in coordinate mondo e non in coordinate immagine:
il rumore sui punti dell'immagine si propaga in maniera non lineare durante la fase di triangolazione e perciò solo in coordinate immagine è possibile supporre che il rumore di individuazione dei punti sia gaussiano a media nulla.
Non è pertanto possibile realizzare uno stimatore a massima verosimiglianza sfruttando solamente i punti in coordinate mondo.
Un approccio più raffinato è quello indicato come 3D-to-2D dove si cerca di minimizzare la riproiezione di un punto del passato in coordinate immagine:
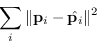 |
(9.89) |
Chiaramente anche questo approccio è inficiato dal fatto che il punto tridimensionale ![]() non è un dato del problema ma è conosciuto con una certa quantità di errore.
Per questa ragione è necessario fare un ulteriore passo minimizzando entrambi gli errori in coordinate immagine (è la Maximum Likelihood Estimation):
non è un dato del problema ma è conosciuto con una certa quantità di errore.
Per questa ragione è necessario fare un ulteriore passo minimizzando entrambi gli errori in coordinate immagine (è la Maximum Likelihood Estimation):
L'odometria visuale è un algoritmo di dead-reckoning e pertanto è affetto da deriva. È possibile estendere questi ragionamenti al caso in cui non siano solo due gli istanti di tempo coinvolti nella minimizzazione ma molteplici. In questo caso si entra in un discorso complicato per cercare di ridurre il più possibile gli errori di deriva nel comporre le diverse trasformazioni. Un tutorial che affronta queste tematiche è (SF11).
Quando si vuole affrontare il problema dal punto di vista bayesiano, sfruttando l'equazione (9.90), e si intendono processare contemporaneamente tutti i fotogrammi, invece che odometria visuale si preferisce parlare di Bundle Adjustment.
Il concetto di Bundle Adjustment, introdotto dalla fotogrammetria e poi acquisito dalla Computer Vision (si veda l'ottimo survey (TMHF00)), indica una minimizzazione multivariabile in modo da ottenere contemporaneamente una ricostruzione tridimensionale, le pose relative della camere in una sequenza di immagini ed eventualmente i parametri intrinseci delle camere stesse.
Si tratta di una estensione alle tecniche non-lineari che stimano i parametri attraverso la minimizzazione di una funzione di costo adeguata basata sugli errori di riproiezione dei punti individuati, nella stessa forma di equazione (9.90).
Siccome la stessa feature può essere vista da diverse immagini, il processo di stima condiziona tutte le pose e di conseguenza il problema non si può scomporre in ![]() problemi separati di odometria visuale:
tutte le immagini della sequenza devono essere minimizzate contemporaneamente.
Per questo motivo il problema della Bundle Adjustment è un problema dimensionalmente elevato, sicuramente non-convesso, che richiede una ottimizzazione non semplice e fa ricorso a minimizzazione sparsa per preservare memoria e migliorare la precisione.
problemi separati di odometria visuale:
tutte le immagini della sequenza devono essere minimizzate contemporaneamente.
Per questo motivo il problema della Bundle Adjustment è un problema dimensionalmente elevato, sicuramente non-convesso, che richiede una ottimizzazione non semplice e fa ricorso a minimizzazione sparsa per preservare memoria e migliorare la precisione.
Un approccio alternativo al Bundle Adjustment, sicuramente non il miglior stimatore alla massima verosimiglianza ma che introduce un numero minore di incognite, è quello del Pose Graph Optimization (GKSB10) che, sfruttando informazione della medesima posa ottenuta da più percorsi ovvero avendo individuato dei Loop, permette di ottimizzare solamente le pose rispetto a quelle ottenute dall'odometria visuale.
Sia
![]() un vettore di parametri dove l'elemento
un vettore di parametri dove l'elemento ![]() rappresenta la posa del nodo i-esimo.
Siano
rappresenta la posa del nodo i-esimo.
Siano
![]() e
e
![]() la misura e la matrice di precisione dell'osservazione virtuale della posa relativa tra i nodi i e j.
L'obiettivo è ottenere una stima dei parametri
la misura e la matrice di precisione dell'osservazione virtuale della posa relativa tra i nodi i e j.
L'obiettivo è ottenere una stima dei parametri ![]() date le osservazioni virtuali
date le osservazioni virtuali
![]() .
Siccome le pose relative vengono ottenute come confronto di due pose assolute, parametri da ottenere, si può definire la funzione costo
.
Siccome le pose relative vengono ottenute come confronto di due pose assolute, parametri da ottenere, si può definire la funzione costo
| (9.91) |
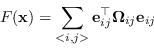 |
(9.92) |
Paolo medici