Next: Rette in Up: Linee, Piani e Iperpiani Previous: Distanza punto-retta
In diversi problemi è necessario conoscere la distanza tra un punto ![]() e una polilinea formata da molteplici segmenti.
Il peso computazionale di questo problema cresce linearmente con il numero di punti con cui è formata la retta: per poter eseguire queste analisi è necessario che il confronto con il singolo punto sia pertanto molto veloce.
e una polilinea formata da molteplici segmenti.
Il peso computazionale di questo problema cresce linearmente con il numero di punti con cui è formata la retta: per poter eseguire queste analisi è necessario che il confronto con il singolo punto sia pertanto molto veloce.
In questa sezione verrà definito come segmento come quella parte di retta limitata tra i punti ![]() e
e ![]() .
Il punto
.
Il punto ![]() e il segmento possono relazionarsi in 3 modi: il punto più vicino è
e il segmento possono relazionarsi in 3 modi: il punto più vicino è ![]() , il punto più vicino è
, il punto più vicino è ![]() o il punto più vicino è un punto compreso tra i due estremi.
Da un punto di vista prettamente computazionale calcolare queste 3 distanze richiederebbe 9 moltiplicazioni, 6 somme e una divisione, oltre ai necessari 3 confronti.
Questa sezione mostra come si può migliorare computazionalmente il confronto facendo uso del prodotto scalare.
o il punto più vicino è un punto compreso tra i due estremi.
Da un punto di vista prettamente computazionale calcolare queste 3 distanze richiederebbe 9 moltiplicazioni, 6 somme e una divisione, oltre ai necessari 3 confronti.
Questa sezione mostra come si può migliorare computazionalmente il confronto facendo uso del prodotto scalare.
Senza perdita di generalità si può supporre che
![]() . Dalla definizione di prodotto scalare
. Dalla definizione di prodotto scalare
| (1.34) |
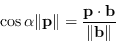 |
(1.35) |
Paolo medici