Next: Modelli a Miscela Up: La distribuzione Gaussiana Previous: La distribuzione Gaussiana
In applicazioni pratiche di elaborazione di segnali discreti, dove la gaussiana viene usata come filtro convolutivo, anche essa deve essere rappresentata a passi discreti ![]() .
La gaussiana viene normalmente campionata a passo uniforme ma, siccome ha supporto infinito, vengono presi tanti campioni per solo 3 o 4 volte la deviazione standard della gaussiana:
.
La gaussiana viene normalmente campionata a passo uniforme ma, siccome ha supporto infinito, vengono presi tanti campioni per solo 3 o 4 volte la deviazione standard della gaussiana:
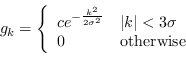 |
(2.18) |
È possibile estendere la gaussiana al caso multidimensionale in modo molto semplice come:
| (2.19) |